- 10,544
- 2,324
Not really a homework question but this is probably the best place to post it.
I'm interested in what people think about the following experiment and the wording of one of the follow up questions that came with it. It was set as part of UK GCSE Physics coursework for the 14-15 age group.
1. Homework Statement
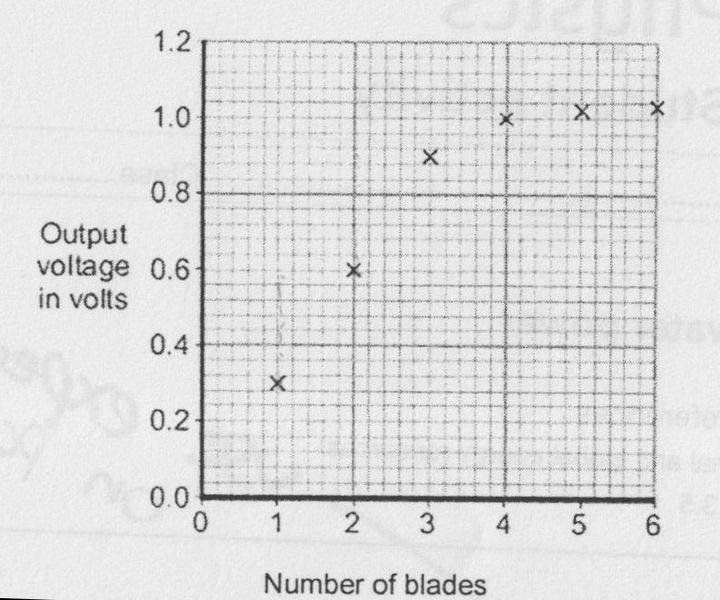
The class was instructed to conduct an experiment that involved setting up a desk fan to blow air at a model wind turbine. The model turbine was connected to a small DC motor and that to a voltmeter. They were asked to change the number of blades on the turbine and plot a graph of voltage against number of blades...
Three related follow up questions were:
3) How many blades do most full-sized modern wind turbines have?
4) What number of blades gives the highest potential difference in the experiment?
5) The number of blades which gives the highest potential difference in this type of experiment is sometimes different from the answer to Question 3. Suggest a reason for this.
None. (This is a basic physics class not an aerodynamics class!)
First two are straightforward.
Q3) 3 blades.
Q4) 6 blades (or perhaps "4 to 6 blades gives the highest potential difference").
My son asked me for advice on how to answer Q5. I can think of possible answers but they aren't expected to know these:
As I recall 3 blades are used for quite technical reasons to do with vibration or resonance but that kind of answer is too advanced for their age range.
Larger turbines are more efficient so need fewer blades? They aren't expected to know that larger blades are more efficient.
More than 3 blades would make the turbine more expensive for little gain? However their experimental data suggests 4 blades would probably be the optimum number.
Large turbines are optimised for maximum power not maximum voltage? (I think).
Is this just a bad question or is there a right answer for this age group that I'm missing?
I'm interested in what people think about the following experiment and the wording of one of the follow up questions that came with it. It was set as part of UK GCSE Physics coursework for the 14-15 age group.
1. Homework Statement
The class was instructed to conduct an experiment that involved setting up a desk fan to blow air at a model wind turbine. The model turbine was connected to a small DC motor and that to a voltmeter. They were asked to change the number of blades on the turbine and plot a graph of voltage against number of blades...
Three related follow up questions were:
3) How many blades do most full-sized modern wind turbines have?
4) What number of blades gives the highest potential difference in the experiment?
5) The number of blades which gives the highest potential difference in this type of experiment is sometimes different from the answer to Question 3. Suggest a reason for this.
Homework Equations
None. (This is a basic physics class not an aerodynamics class!)
The Attempt at a Solution
First two are straightforward.
Q3) 3 blades.
Q4) 6 blades (or perhaps "4 to 6 blades gives the highest potential difference").
My son asked me for advice on how to answer Q5. I can think of possible answers but they aren't expected to know these:
As I recall 3 blades are used for quite technical reasons to do with vibration or resonance but that kind of answer is too advanced for their age range.
Larger turbines are more efficient so need fewer blades? They aren't expected to know that larger blades are more efficient.
More than 3 blades would make the turbine more expensive for little gain? However their experimental data suggests 4 blades would probably be the optimum number.
Large turbines are optimised for maximum power not maximum voltage? (I think).
Is this just a bad question or is there a right answer for this age group that I'm missing?