beefcake466
- 9
- 0
please help with static equillibrium TEE exam in a few days
hi I've got a physics question that is static equillibrium, if anyone can help me sort out the prob i would be very happy :).
ok the prob i have with it is i get the cos or sin the angle wrong like i get everythign else right exept i get the cos or sin mixed up, if anyone can tell me how i determine which one to use it woul be very nice.
FIND THE TENSION in cable
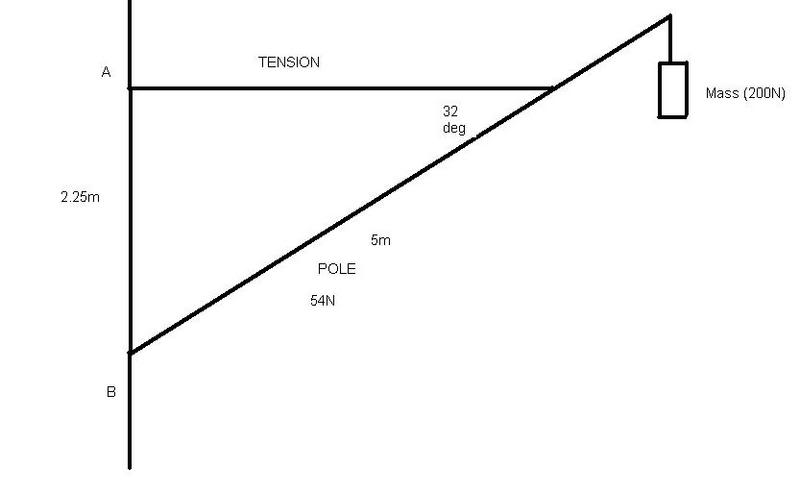
hi I've got a physics question that is static equillibrium, if anyone can help me sort out the prob i would be very happy :).
ok the prob i have with it is i get the cos or sin the angle wrong like i get everythign else right exept i get the cos or sin mixed up, if anyone can tell me how i determine which one to use it woul be very nice.
FIND THE TENSION in cable