- #1
maniacp08
- 115
- 0
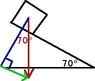
A 8 kg block slides down a frictionless incline making an angle of 70° with the horizontal.
(a) What is the total work done on the block when the block slides 2 m (measured along the incline)?
(b) What is the speed of the block after it has slid 1.5 m if it starts from rest?
m/s
(c) What is its speed after 1.5 m if it starts with an initial speed of 2 m
relevant equations:
Work = Force * Cos Theta * Displacement
Total Work = change in Kinetic Energy
There are two forces acting on the block, the normal force and force of gravity.
The normal force will do no work because it is perpendicular to the displacement.
So the net force will be the force of gravity?
Which is:
(8kg)(9.81m/s^2) * Cos (-160) * 2m = -147.5J
Please correct me if I am wrong anywhere. Thanks.
(a) What is the total work done on the block when the block slides 2 m (measured along the incline)?
(b) What is the speed of the block after it has slid 1.5 m if it starts from rest?
m/s
(c) What is its speed after 1.5 m if it starts with an initial speed of 2 m
relevant equations:
Work = Force * Cos Theta * Displacement
Total Work = change in Kinetic Energy
There are two forces acting on the block, the normal force and force of gravity.
The normal force will do no work because it is perpendicular to the displacement.
So the net force will be the force of gravity?
Which is:
(8kg)(9.81m/s^2) * Cos (-160) * 2m = -147.5J
Please correct me if I am wrong anywhere. Thanks.