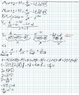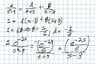- #1
s3a
- 818
- 8
Homework Statement
Solve the differential equation y'' - 9y = 4t - δ_2(t); y() = -2, y'(0) = -1 for y(t) when 0 <= t < 2 as well as when t > 2.
Homework Equations
Dirac delta function. Heaviside function. Laplace and Inverse Laplace Transforms.
The Attempt at a Solution
I'll type the relevant information here since my handwriting for my work is ugly (but I am uploading it anyways just in case you need it). I get to Y(s) = 4/[s^2 * (s^2 - 9)] - e^(-2s)/(s^2 - 9) - (2s+1)/(s^2 - 9) and I'm stuck at getting the inverse Laplace Transform of the bolded/italicized term. Could someone please show me how to do that part? I know it involves the unit step/Heaviside function but I don't know what to do specifically.
From Wolfram Alpha,
The inverse Laplace Transform of that bolded/italicized term is:
http://www.wolframalpha.com/input/?i=inverse+laplace+transform+of+{-exp(-2s)/(s^2+-+9)}
The inverse Laplace Transform of the whole (s) = 4/[s^2 * (s^2 - 9)] - e^(-2s)/(s^2 - 9) - (2s+1)/(s^2 - 9) equality is:
http://www.wolframalpha.com/input/?i=inverse+laplace+transform+of+{4/[s^2+*+(s^2+-+9)]+-+exp(-2s)/(s^2+-+9)+-+(2s%2B1)/(s^2+-+9)}
(Just to note, the Wolfram Alpha answers would be wrong if my work leading up to the equation I retyped in this forum post from my work is incorrect.)
Thanks in advance!