Yet another projectile motion question - for practical writeup

[shichi_reifujin]

I am having no luck with my writeup. We did two related practicals: shot a rocked straight up to find the height, and then shot out at angles to obtain a range.

For the first one, two angles were obtained using a clinometre, then averaged:
d = 30
θ = 60, 69
Av. θ = 64.5

d = 60
θ = 46, 32
Av. θ = 39

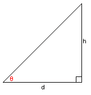
From there, h (see attached diagram) was worked out:
Tan64.5 = h/30
h = 30 x Tan64.5
h = 64.9m

Tan39 = h/60
h = 60 x Tan39
h = 48.6m

This is what's confusing me. How do these measurements relate to projectile motion? What am I supposed to be working out with them?

The next part of the practical involved finding the maximum range. I have the results, but I'm not sure exactly what I'm supposed to be finding with them. We were required to research projectile motion ourselves, and I'm guessing I'm in over my head. Any help would be greatly appreciated, so thank you in advance!

 

[andrevdh]

Sichi, look in your handbook for the part on shooting the monkey. It should be under projectile motion.

Here is a link to a short explanation of it:
http://physics.ucr.edu/~wudka/Physics7/Notes_www/node50.html"

 

[shichi_reifujin]

Shooting the monkey? There's nothing in my textbook on projectile motion. We actually don't cover it until next year, but my teacher decided to "give us a head start". *shakes head*

I'll take a look at the page, and see how I go from there.

 

[andrevdh]

Yes, I agree it is a bit unfair to expect you to do projectile motion on your own. Try to speak to students who have treated projectile motion, or have a look at their handbook.

Have you done linear motion with a constant acceleration yet?

What about vectors and components?

 

[shichi_reifujin]

I took a look at the textbook used next year for Physics. It's in there, but I'm still not really understanding it. We've done both linear motion and vectors and components already.

I'll ask the guy who I borrowed the textbook from and see how I go. I think my main problem is that I can't see how my results relate to anything...

 

[andrevdh]

Can you relate the calculated height to the "shooting the monkey" problem? Hint: Look at the link I provided.