Yo-Yo on a table contradiction

[Order]

Homework Statement

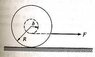
A Yo-Yo of mass M has an axle of radius b and a spool of radius R. Its moment of inertia can be taken to be MR²/2. The Yo-Yo is placed upright on a table and the string is pulled with a horizontal force F as shown. The coefficient of friction between the Yo-Yo and the table is mu.
What is the maximum value of F for which the Yo-Yo will roll without slipping? (See thumbnail below)

Homework Equations

$$F=Ma$$
$$\tau=I\alpha$$

The Attempt at a Solution

I have no idea. Neverhteless I can show the equations. Firstly I have the Newtons second law $$F-\mu Mg=Ma,$$ where $$F\ge \mu Mg,$$ so that it does not move backwards with a forward force. Secondly I have the equation $$\mu MgR-Fb=I\alpha,$$ where $$Fb\ge \mu MgR,$$ so that it does not roll forward with a backward pull.

Now using the moment of inertia and $$a=\alpha R,$$ I have $$\mu Mgr-Fb=I\alpha=\frac{RMa}{2}$$ and putting the equations together $$F-\mu Mg=2 \mu Mg-\frac{2Fb}{R}.$$

But this is a contradiction because in the constraint that i used the right hand side of this equation is never negative whereas the right hand side is never positive. The only solution is that both are zero. So the condition that the Yo-Yo should not slide is $$F=\mu Mg.$$ But this contradicts my second constraint that $$Fb\ge \mu MgR,$$ because b<R. The solution must then be that the pull should not exceed the friction force, which is variable. But this is not correct. So where does my thinking go bananas?

 

[ehild]

Firstly I have the Newtons second law $$F-\mu Mg=Ma,$$ where $$F\ge \mu Mg,$$ so that it does not move backwards with a forward force. Secondly I have the equation $$\mu MgR-Fb=I\alpha,$$ where $$Fb\ge \mu MgR,$$ so that it does not roll forward with a backward pull.

When the yo-yo rolls there is static friction between it and the ground: Fs<=μmg. So the first equation should be

F-Fs=Ma,
where a is the acceleration of the CM.

Considering the torques with respect the CM, that of F causes rolling backwards, and the torque of static friction causes the yo-yo rolling forward. So

Fs*R-b*F=I*a/R.

Cancel Fs, find a, and replacing back into the first equation, you get the relation between Fs and F. Use that Fs<μmg to get an upper limit for F.

 

[Order]

When the yo-yo rolls there is static friction between it and the ground: Fs<=μmg. So the first equation should be

F-Fs=Ma,
where a is the acceleration of the CM.

Considering the torques with respect the CM, that of F causes rolling backwards, and the torque of static friction causes the yo-yo rolling forward. So

Fs*R-b*F=I*a/R.

Cancel Fs, find a, and replacing back into the first equation, you get the relation between Fs and F. Use that Fs<μmg to get an upper limit for F.

Ok, thanks for reply! I use $$F-F_{s}=Ma$$ and $$Fb-F_{s}R=I\alpha=-\frac{RMa}{2}$$ and put these two equations together: $$F-F_{s}=2F_{s}-\frac{2Fb}{R}$$ which leads to the relation $$F=\frac{3F_{s}R}{R+2b}$$ where $$F_{s}\le \mu Mg$$ That is the right order to solve the problem, so thanks for help. But there is still an important problem. I don't have a real Yo-Yo to perform an experiment with, but is it true that it then will accelerate to the right without slipping. According to the equations this should be so because $$Ma=F-F_{s}=\frac{3F_{s}R}{R+2b}-F_{s}=F_{s}\frac{2R-2b}{R+2b}$$ which is obviously greater than zero. This is really confusing to me and the reason I have been thinking about this problem for over a week. Could someone please tell me what really happens?

 

[ehild]

It will roll in the direction of the pull unless the pulling force is too strong. You do no need a yo-yo for the experiment: a cotton reel will do. It is even better than the yo-yo. The yo-yo is too thin and unstable. I think you can find a reel. Your mother, grandmother, aunt, wife, sister, daughter must have such thing.
You got the condition for F assuming that the yo-yo accelerated on the right without slipping. No wonder, that you get such acceleration at the end. It means that your solution was correct.

ehild

 

[Order]

It will roll in the direction of the pull unless the pulling force is too strong. You do no need a yo-yo for the experiment: a cotton reel will do. It is even better than the yo-yo. The yo-yo is too thin and unstable. I think you can find a reel. Your mother, grandmother, aunt, wife, sister, daughter must have such thing.
You got the condition for F assuming that the yo-yo accelerated on the right without slipping. No wonder, that you get such acceleration at the end. It means that your solution was correct.

ehild

Thanks again! I tried the experiment and was amazed at how quickly the reel responds to the force. Of course it is very light (and I am very heavy I must confess). Then when the force is too strong the angular momentum becomes zero or oscillates around zero. I guess when it slides there is no static friction by which the torque can develop, but why it oscillates is something i need to think about.

 

[ehild]

That oscillation is interesting, I never experienced it! How does the reel move then?
I have got only cotton-reels, what about trying with a heavy thing, cable-reel, for example?

When sliding, the force of friction is kinetic, Fk=μmg. You get two separate equation for the acceleration of the CM and for the angular acceleration around the CM, but you need to know the direction of friction. If it is backwards, the angular acceleration can have both signs, according to the magnitude of F. You can find both the
velocity of CM and the angular velocity. From these, get the velocity of the lowest point of the yo-yo. The force of friction opposes this velocity, it can act forward and backward, accordingly.

Let me know if you have new experimental results!

ehild

 

[Order]

That oscillation is interesting, I never experienced it! How does the reel move then?
I have got only cotton-reels, what about trying with a heavy thing, cable-reel, for example?

When sliding, the force of friction is kinetic, Fk=μmg. You get two separate equation for the acceleration of the CM and for the angular acceleration around the CM, but you need to know the direction of friction. If it is backwards, the angular acceleration can have both signs, according to the magnitude of F. You can find both the
velocity of CM and the angular velocity. From these, get the velocity of the lowest point of the yo-yo. The force of friction opposes this velocity, it can act forward and backward, accordingly.

Let me know if you have new experimental results!

ehild

I found it difficult to keep the reel straight and even more difficult to repeat the experiement, but what I saw was an oscillation around the horizontal axis, not the vertical axis and without any sign of decreasing. So your thought that it is due to changing signs might be it. I find it difficult to apply it mathematically though.

I will try it on a heavier reel as soon as I find one.