palaphys
- 266
- 17
- Homework Statement
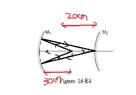
- A converging mirror M1, a point source S and a diverging
mirror M2 are arranged as shown in figure (18-E4). The
source is placed at a distance of 30 cm from M1. The
focal length of each of the mirrors is 20 cm. Consider
only the images formed by a maximum of two reflections.
It is found that one image is formed on the source itself.
(a) Find the distance between the two mirrors. (b) Find
the location of the image formed by the single reflection
from M2 .
- Relevant Equations
- 1/v+1/u=1/f
There is the figure provided.
I know how to approach this problem analytically, but before that I tried to use some logic-
Using mirror formula assuming the first reflection occurs at M1, we get that the first image is formed at a distance ##60 cm## from the pole of M1 to its left.
So, if this image was formed EXACTLY at center of curvature of the diverging mirror, then the angle of incidence would be equal to the angle of reflection, both equal to zero, as the rays would be incident normally, and the next image would be formed at S again.
Here's a diagram of what I mean:
so from here we can say that the distance between the mirrors would be ##20cm##, right? but the analytical method yields a solution as ##50cm## which is the correct ans.
Thinking further, why can't the distance between the mirrors be ##60 cm## itself? If the image from the first reflection of M1 is formed at the pole of M2, then the reflected rays will pass symmetrically as shown, leading to the image and object coinciding as shown in the figure:
But why is this wrong as well?