Truss compression and tension forces help

gozita73
Messages
15
Reaction score
0
The space truss showin has compression and tension forces acting in the members as shown.

t6pfg1.png


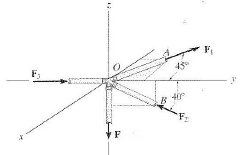
Force F is 10kN, determine the three unknown forces (F1, F2 and F3).


I know that it should be the summation of Fx, Fy and Fz, however for F1, there is no reaction force, so I don't know what to do.

Can somebody please help?
 
Physics news on Phys.org
Attach A & B to a vertical wall.
What force is needed directly on the wall at the level of F3 to stop the wall from being pulled over by F.
 
so the x component of F1 would be supported by the wall??
 
bump ?
 
gozita73 said:
so the x component of F1 would be supported by the wall??
I'm not too good looking at 3D, but something appears wrong with your picture. There appears to be no way for the x component of the F1 force to be balanced at the joint, since the other 3 members all lie in the yz plane, unless the picture is misleading or incomplete?
 

Thread 'Initial conditions for orbits around a wormhole'

Hi, I had an exam and I completely messed up a problem. Especially one part which was necessary for the rest of the problem. Basically, I have a wormhole metric: $$(ds)^2 = -(dt)^2 + (dr)^2 + (r^2 + b^2)( (d\theta)^2 + sin^2 \theta (d\phi)^2 )$$ Where ##b=1## with an orbit only in the equatorial plane. We also know from the question that the orbit must satisfy this relationship: $$\varepsilon = \frac{1}{2} (\frac{dr}{d\tau})^2 + V_{eff}(r)$$ Ultimately, I was tasked to find the initial...
View full post »

Thread 'Help to convert units of a simple formula'

The value of H equals ## 10^{3}## in natural units, According to : https://en.wikipedia.org/wiki/Natural_units, ## t \sim 10^{-21} sec = 10^{21} Hz ##, and since ## \text{GeV} \sim 10^{24} \text{Hz } ##, ## GeV \sim 10^{24} \times 10^{-21} = 10^3 ## in natural units. So is this conversion correct? Also in the above formula, can I convert H to that natural units , since it’s a constant, while keeping k in Hz ?
View full post »

Similar threads

How to check the Stability of ANY Truss?
Replies
1
Views
2K
Statics - Compression and tension forces in a truss
Replies
2
Views
6K
Truss Bridge Tension and Compressions
Replies
3
Views
22K
How to calculate the magnitudes of three forces around a hexagon
Replies
17
Views
2K
How Do You Calculate Forces in Truss Members?
Replies
1
Views
2K
Truss Analysis using joints method 2D analysis
Replies
1
Views
2K
Help understanding how to determine Compress or Tension in Truss
Replies
3
Views
7K
How to Determine the Magnetic Field B Using Forces F1, F2, and F3 on a Charge?
Replies
1
Views
2K
Plotting the graph of Friction Force vs. time (Laws of motion)
Replies
1
Views
2K
Equilibrium problem: Multiple forces acting on this hinged, supported beam
Replies
3
Views
1K

Hot Threads

Recent Insights

Back
Top