callawee
- 2
- 0
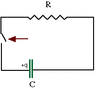
In the circuit below, the time required (s) for the charge on the capacitor to drop to 47% of its value after the switch is closed is 2.83 s. If R = 1340 ohms, what is C in μF (microfarad)?
(dq/dt) + q/(RC) = 0
(.47q)/(t) = q/(RC)
t/(.47R)= C
Convert C from F to uF by multiplying by 10^6
I am getting 4993 uF, but that is the wrong answer and I'm not sure where I'm going wrong. Thanks for any help.
(dq/dt) + q/(RC) = 0
(.47q)/(t) = q/(RC)
t/(.47R)= C
Convert C from F to uF by multiplying by 10^6
I am getting 4993 uF, but that is the wrong answer and I'm not sure where I'm going wrong. Thanks for any help.