morsel
- 29
- 0
Homework Statement
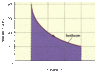
Suppose 161 moles of a monatomic ideal gas undergoes an isothermal expansion as shown in the figure (attached). The horizontal axis is marked in increments on 20 m3
What is the temperature at the beginning and at the end of this process?
Homework Equations
PV = nRT
The Attempt at a Solution
Pi = 400 kPa
Vi = 20 m3
Pf = 100 kPa
Vf = 80 m3
T = (PV)/(nR) = (400*20)/(161*8.31) = 5.98 K
My answer is wrong according to the online homework grading system. What am I doing wrong?
Any help is appreciated.