Find Function R(z) for Coin Rolling in Funnel

[jaykay99]

Homework Statement

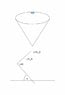
A coin(radius=r) rolls in a funnel only with a horizontal speed v. The coin always stays at his altitude.
The coin has a homogen mass distribution and it only rolls! So it has a translational motion and a rotation motion.
Find a function R(z) whitch discribes the form of the funnel!
R>>r and z is the altitude of the funnel. the z-coordinate of the coin is changeless.

Homework Equations

I thougth it must be \tan\alpha=\frac{v^2}{r\cdot g}

But then i tought the speed at all parts of the coin isn't the same.

If there are any questions in understand my problem, ask!
I made a drawing of that:

Can u pls help me?
Thank you

 

[Quinzio]

But then i tought the speed at all parts of the coin isn't the same.

Every wheel that rolls on a surface behaves like that and its velocity is the velocity of the center.
Your equation is ok, but the problem asks to have it as a function of z, not of the radious (r).

But anyway I think in a real world experiment, it will not work, can you see why ? (tell your professor!)

 

[jaykay99]

If there is no friction, it could work.

Because the speed is not constant the F_z also is not constant. So it would be more difficult.

Or other question:
What is the difference between a pointmass and a coin rolling like this?

When a point rolls like this it is quite easy to get R(z) or Z(r) cause they are inverse functions.

 

[jaykay99]

is it too difficult?
Should i put in advanced physics?

 

[Quinzio]

If there is no friction, it could work.

Because the speed is not constant the F_z also is not constant. So it would be more difficult.

Or other question:
What is the difference between a pointmass and a coin rolling like this?

When a point rolls like this it is quite easy to get R(z) or Z(r) cause they are inverse functions.

No, it's not a problem of friction.
If you think the coin as a flat cylinder, the axis of the cylinder will have to rotate in order to form always the same angle with the surface of the funnell.

The coin rolls about his axis, but the axis must make a precession like movement (as if it was a spinning top).
It will behave like a gyroscope.
If the precession velocity of the gyroscope is not the same of the angular velocity of the coin around the funnell, then the coin will finally fall or follow an erratic path.

For your problem you are ok, the answer you gave is correct, I think that the gyrscope behaviour is advanced for your class.
In real world that coin would make an erratic path.

 

[jaykay99]

Thank you for your answer.
I found a nice vid on youtube: https://www.youtube.com/watch?v=http://www.youtube.com/watch?v=rfyng8f-bOA&feature=related

What form must the funnel have?
Is it really to complicated to calculate with the gyrscope behaviour?