Double integrals - Change of variables

[NewtonianAlch]

Homework Statement

Find the area in the positive quadrant of the x-y plane bounded by the curves ${x}^{2}+2\,{y}^{2}=1$, ${x}^{2}+2\,{y}^{2}=4$, $y=2\,x$, $y=5\,x$

The Attempt at a Solution

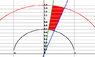
This is a graph of the region:

http://img21.imageshack.us/img21/2947/59763898.jpg

One thing I was confused about in regards to the domain was which part to specifically shade in, since there are two ellipses here. I can see that the relevant area is in between the two lines, but now there are two boundaries due to the ellipses. I'm guessing it's in the inner one, and not both, because the smaller ellipse doesn't contain anything outside it.

For the substitutions I thought of $u = {x}^{2}+2\,{y}^{2}$ and $v = {\frac {y}{x}}$

Calculating the Jacobian of this gives us $2+4\,{\frac {{y}^{2}}{{x}^{2}}}$

This is where I'm stuck as I'm not sure how to get this into a form (in terms of u and v) to put in the integral.

I considered using polar substitution, but that seems to be messier.

 

[DryRun]

See the attached graph to this post. The area that you need to find is shaded in red.

You just solve using polar coordinates. Express all the 4 equations in polar form.

$$\int^{\arctan 5}_{\arctan 2} \int^{\frac{2}{\sqrt{1+\sin^2 \theta}}}_{\frac{1}{\sqrt{1+\sin^2 \theta}}} rdrd\theta$$

To integrate w.r.t.$\theta$, use substitution: Let $\sin \theta = \tan \phi$.

Using (x,y) to (u,v) transformations might also work. In that case, your Jacobian is wrong.
$$J= \frac{\partial (u,v)}{\partial (x,y)}=2x+\frac{4y^2}{x^2}$$
$$dxdy=\frac{x^2}{2x^3+4y^2}dudv$$
Now, to get the limits of the new integral, you should plot the u-v lines. See the second attached graph.

Convert $\frac{x^2}{2x^3+4y^2}$ in terms of u an v, and replace as the integrand below.

$$\int^5_2 \int^4_1 \frac{x^2}{2x^3+4y^2} \,.dudv$$

 

[LCKurtz]

You can change the problem to integrating over a sector between two circles with the substitution $u=x,\ v=y\sqrt 2$.

 

[DryRun]

You can change the problem to integrating over a sector between two circles with the substitution $u=x,\ v=y\sqrt 2$.

Hi LCKurtz

I suppose your method makes the integration less tedious. But how did you derive those substitutions?

 

[Mark44]

From the 2y² terms in the ellipses. This change and the other one convert the ellipses in the x-y plane to circles in the u-v plane.

 

[LCKurtz]

You can change the problem to integrating over a sector between two circles with the substitution $u=x,\ v=y\sqrt 2$.

Hi LCKurtz

I suppose your method makes the integration less tedious. But how did you derive those substitutions?

You want to make $x^2+2y^2$ become $u^2+v^2$. It not only makes the integration less tedious, it eliminates it completely if you use the well known formula for the area of a sector of a circle.

 

[DryRun]

OK, using the suggestion above, it is not possible to find the Jacobian in this case.

Plotting the graph of: $u^2+v^2=1$, $u^2+v^2=4$, $v=2\sqrt2 u$ and $v=5\sqrt2 u$. I have attached the graph to this post.

So, i end up with a pair of concentric circles. Now, using the formula for finding the area of sector of a circle: $$A= \frac{1}{2}r^2 \theta$$
I know that $1\le r \le 2$ for the area of region required in the u-v plane. Since, $\theta$ is the same for both sectors:

Area of required region=$$\frac{1}{2}(2)^2 \theta-\frac{1}{2}(1)^2 \theta=\frac{3}{2}\theta$$ But i have no idea how to find $\theta$.

 

[LCKurtz]

OK, using the suggestion above, it is not possible to find the Jacobian in this case.
$du=dx$ and $dv=\sqrt2dy$.
Plotting the graph of: $u^2+v^2=1$, $u^2+v^2=4$, $v=2\sqrt2 u$ and $v=5\sqrt2 u$. I have attached the graph to this post.

So, i end up with a pair of concentric circles. Now, using the formula for finding the area of sector of a circle: $$A= \frac{1}{2}r^2 \theta$$

I know that $1\le r \le 2$ for the area of region required in the u-v plane. Since, $\theta$ is the same for both sectors...

Of course you can calculate the Jacobian. But remember, this question was posted by NewtonianAlch, and you should be careful not to provide a full solution.

 

[DryRun]

Of course you can calculate the Jacobian. But remember, this question was posted by NewtonianAlch, and you should be careful not to provide a full solution.

I will try to skip the obvious steps. The method you suggested is new to me, as I've not encountered substitution of the (x, y) variables by (u, v). Usually, u and v are substitutes for the real constants parts.

So, $dxdy=\frac{1}{\sqrt2}dudv$

The final integral for the area of the required section is: $$\frac{1}{\sqrt 2}\int^2_1 \int^{\sqrt{4-v^2}}_{\sqrt{1-v^2}} \,.dudv$$
Is that correct? Unfortunately, i haven't used the area of sector, so maybe i missed the point.

EDIT: OK, after some more thinking, considering the curves and lines in the u-v plane and finding the points of intersection of the inner circle and lines:
$u^2+v^2=1$ and line $v=2\sqrt2u$ which is $(\frac{1}{3},{2\sqrt2}{3})$, and gives $\theta = \arctan (2\sqrt2)$
$u^2+v^2=1$ and line $v=5\sqrt2u$ which is $(\frac{2}{\sqrt{51}},\frac{10\sqrt2}{\sqrt{51}})$, and gives $\theta = \arctan (\frac{10}{\sqrt2})$
The angle $\phi$ between $v=5\sqrt2 u$ and $v=2\sqrt2 u$ is: $\arctan (\frac{10}{\sqrt2})-\arctan (2\sqrt2)$

Hence, area of region = $\left[ \frac{1}{2}(2)^2 \phi \right]-\left[ \frac{1}{2}(1)^2 \phi \right]=\frac{3}{2}\phi$
I hope this is correct? If yes, then there is no need to find the Jacobian at all?

 

[LCKurtz]

Almost, but you left the Jacobian out of your final answer. The Jacobian is the absolute value of$$
\frac{\partial(x,y)}{\partial(u,v)}=\left | \begin{array}{cc}
x_u&x_v\\y_u&y_v\end{array}\right|
=\left | \begin{array}{cc}
1&0\\0&\frac {1} {\sqrt 2}\end{array}\right |=\frac 1 {\sqrt 2}$$

 

[DryRun]

I think the best way to think about this is:
Cartesian (x,y) coordinates -> (u,v) coordinates -> Polar coordinates.
The part where i evaluated the area of the required section should have been a double integral: $$\iint rdrd\theta$$ but using the area of sector proved to be a simpler method.

 

[LCKurtz]

I think the best way to think about this is:
Cartesian (x,y) coordinates -> Cartesian (u,v) coordinates -> Polar coordinates.
The part where i evaluated the area of the required section should have been a double integral: $$\iint rdrd\theta$$ but using the area of sector proved to be a simpler method.

Yes, you can certainly do that and that is where the formula for the area of a sector comes from. It's just a question of what you want to take as already "known" and what you need to prove. By the way, have you noticed that the $r$ in $rdrd\theta$ is just the Jacobian of the transformation $x = r\cos\theta,\ y = r\sin\theta\$, which is why you can use the substitution $dydx =r dr d\theta\$?

 

[DryRun]

By the way, have you noticed that the $r$ in $rdrd\theta$ is just the Jacobian of the transformation $x = r\cos\theta,\ y = r\sin\theta\$, which is why you can use the substitution $dydx =r dr d\theta\$?

It's not obvious, but you are right. The Jacobian checks out.

From my book, (u,v) is called the curvilinear coordinate system, however from this problem, it appears that the curvilinear coordinate system shares the same characteristics as the Cartesian coordinate system? When converting from curvilinear coordinates to polar coordinates, i just used the same method as i would when converting from Cartesian coordinates to polar coordinates, that is, by finding the Jacobian, etc.

 

[NewtonianAlch]

Oh dear...I wouldn't be too worried about having inadvertently posted "full solutions" because I can't make heads or tails out of this anyhow.

Thanks for the posts, so I take it there are 2 ways (at least in this thread) to go about this, and depending on the substitution you pick, it can make the integration harder or easier to complete?

 

[LCKurtz]

Oh dear...I wouldn't be too worried about having inadvertently posted "full solutions" because I can't make heads or tails out of this anyhow.

Thanks for the posts, so I take it there are 2 ways (at least in this thread) to go about this, and depending on the substitution you pick, it can make the integration harder or easier to complete?

What you should do is try the substitution I gave in post #3. Its Jacobian is calculated in post #10. Change the x-y integral to a u-v integral. See if you can see that in the u-v plane you get a region between two circles instead of two ellipses. See what the equations of the two straight lines become in u-v. Once you figure that out you will have an integral over a nice region that you can either do in polar coordinates or just use standard formulas for the areas of sectors of a circle.

 

[NewtonianAlch]

I will try that now thanks, was trying to figure what the best way was to go about it. Thanks for the pointers.

 

[NewtonianAlch]

Although, shouldn't that Jacobian be:

$\left[ \begin {array}{cc} 1&0\\ \0&\sqrt {2} \end {array} \right]$

 

[DryRun]

Although, shouldn't that Jacobian be:

$\left[ \begin {array}{cc} 1&0\\ \0&\sqrt {2} \end {array} \right]$

No, the Jacobian is finding the determinant. What do you mean by \0?
See post #10: https://www.physicsforums.com/showpost.php?p=3898197&postcount=10

 

[Tayyabah]

Hi!

I have a similar Problem.

I have to calculate the double integral given below.

∬D√(x2 +y2) dxdy, D=x2+y2≤2x

How can i calculate the limits from the give inequality to calculate the value of the given double integral?

Waiting for a kind response.

Thanks in advance

 

[DryRun]

Hi!

I have a similar Problem.

I have to calculate the double integral given below.

∬D√(x2 +y2) dxdy, D=x2+y2≤2x

How can i calculate the limits from the give inequality to calculate the value of the given double integral?

Waiting for a kind response.

Thanks in advance

LOL! You might really get banned this time. Your previous posts were deleted by the moderator/s for the same reasons; read the forum rules before posting anything anywhere on the forums.

 

[LCKurtz]

Hi!

I have a similar Problem.

I have to calculate the double integral given below.

∬D√(x2 +y2) dxdy, D=x2+y2≤2x

How can i calculate the limits from the give inequality to calculate the value of the given double integral?

Waiting for a kind response.

Thanks in advance

You should start a new thread instead of posting a new question in an ongoing thread. I see that you have apparently figured that out since you did start a new thread.

 

[NewtonianAlch]

I sketched the circle in u and v and the two lines, it's similar to the diagram with the ellipse.

The radii are 1 and √4 = 2

So we have an integral going from:

$$\int^{\arctan 5√2}_{\arctan 2√2} \int^{2}_{1}$$

The Jacobian I calculated to be $√2r$

For some reason I think I'm calculating this Jacobian differently? I didn't get this:

$$\frac 1 {\sqrt 2}$$

I tried it on MAPLE, and this is the output I got for the Jacobian, for (u = r cos (x) and v = sqrt(2)*r sin(x))

$\left[ \begin {array}{cc} \cos \left( x \right) &-r\sin \left( x \right) \\ \sqrt {2}\sin \left( x \right) &\sqrt {2 }r\cos \left( x \right) \end {array} \right]$Evaluating this I get:

$(3/2)*sqrt(2)*(arctan(5*sqrt(2))-arctan(3*sqrt(2)))$

Whereas the final answer is the same thing, except (3/4).

 

[NewtonianAlch]

No, the Jacobian is finding the determinant. What do you mean by \0?
See post #10: https://www.physicsforums.com/showpost.php?p=3898197&postcount=10

Sorry, formatting problem with MAPLE. It's just 0.

 

[LCKurtz]

I sketched the circle in u and v and the two lines, it's similar to the diagram with the ellipse.

The radii are 1 and √4 = 2

So we have an integral going from:

$$\int^{\arctan 5√2}_{\arctan 2√2} \int^{2}_{1}$$

The Jacobian I calculated to be $√2r$

One thing at a time. You changed the integral to a du dv integral, and those limits are not the u v limits. Your step after the change of variables should look like$$
\iint_R |J|dudv = \iint_R \frac 1 {\sqrt 2}dudv$$ where $R$ is the region in the uv plane you say you have sketched. I showed the calculation of $J$ in post #10.

At this point you can either change from uv to polar coordinates, which will use the $r$ and $\theta$ limits you have figured out above, or just use the formula for the area of a sector of a circle by subtracting the small sector from the larger one.