Finding Partial Derivatives of a Multivariable Function

[geekba]

Hi!
Here is my function:

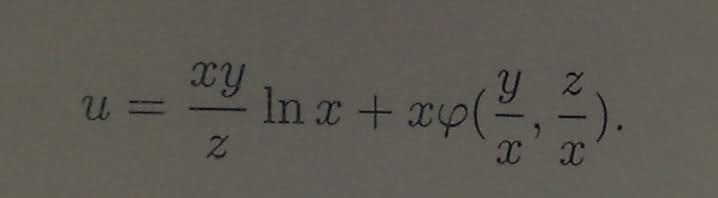
My task is to find:

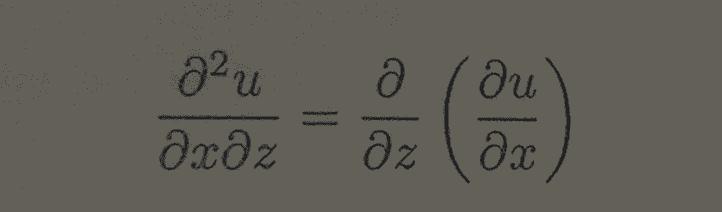
I think I know how to find ∂u/∂x, but I have no idea how to find ∂/∂z(∂u/∂x). Here is how I found ∂u/∂x:

http://oi48.tinypic.com/prsly.jpg

Does someone know how to find ∂/∂z(∂u/∂x)?
I appreciate any help :)

 

[Sourabh N]

Before the second partial derivative, you should fix the error in your calculation of ∂u/∂x, specifically ∂(\frac{xy}{z})/∂x.

 

[geekba]

What's wrong with ∂(xy/z)/∂x? I checked it and it seems correct to me...

 

[geekba]

It's very important so all suggestions are welcome :)

 

[Sourabh N]

What's wrong with ∂(xy/z)/∂x? I checked it and it seems correct to me...

Never mind. I hadn't scrolled all the way down, it is correct.

I believe you are having trouble calculating \frac{∂}{∂z}(∂\rho/∂s) and \frac{∂}{∂z}(∂\rho/∂t) (Let me know if this is not the case).
To simplify this, get rid of s and t by writing ∂\rho/∂s and ∂\rho/∂t as partial derivatives of \rho w.r.t. x, y and z, using the chain rule. Since you know how s and t depend on x, y and z, this can be done.

Once you have done this, calculating \frac{∂}{∂z}(∂\rho/∂s) and \frac{∂}{∂z}(∂\rho/∂t) would be straightforward.

 

[geekba]

I got it finally Thaks a lot!