rishch
- 106
- 1
Refraction -- A fish under water
1 A fish under water obliquely sees a fisher-man standing on the bank of a lake. How does he appear?
2 A parallel sided glass plate is introduced in the path of a converging beam. What happens to the point of convergence of the beam?
It's not that I don't know how to solve these questions it's just that my answer differs from the one the textbook gives.
1 The textbook answer is that he appears taller than he actually is. Why? I thought that he would appear a bit higher than he actually is due to normal shift?
2 Textbook answer is that the point of convergence shifts towards the glass plate. But when I visualize, I think that it moves further away from the glass plate.
Homework Statement
1 A fish under water obliquely sees a fisher-man standing on the bank of a lake. How does he appear?
2 A parallel sided glass plate is introduced in the path of a converging beam. What happens to the point of convergence of the beam?
The Attempt at a Solution
It's not that I don't know how to solve these questions it's just that my answer differs from the one the textbook gives.
1 The textbook answer is that he appears taller than he actually is. Why? I thought that he would appear a bit higher than he actually is due to normal shift?
2 Textbook answer is that the point of convergence shifts towards the glass plate. But when I visualize, I think that it moves further away from the glass plate.
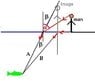
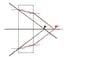
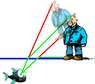
 The whole world above the water appears inside some smaller viewing angle, everything shrinks, so must the man, but to know the image exactly, we have to draw at least two rays from every point.
The whole world above the water appears inside some smaller viewing angle, everything shrinks, so must the man, but to know the image exactly, we have to draw at least two rays from every point.