agro
- 46
- 0
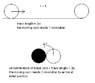
Imagine rolling a coin with a radius of 1 unit on a flat surface. To get translated 2[pi] units, the coin must obviously roll 1 revolution. (the angle swept is 2[pi] and the arc length covered equals to 2[pi]*r = 2[pi]*1 = 2[pi].
Now imagine rolling a coin on another stationary coin with the same radius (circumference = 2[pi] = length of the first track). How can it be that it requires 2 revolutions? Is it because the real track isn't the black coin but the trace of the circle's center when moving (which equals 4[pi])?
It makes me feel uneasy... Can anyone give a satisfactory/intuitive explanation?
Now imagine rolling a coin on another stationary coin with the same radius (circumference = 2[pi] = length of the first track). How can it be that it requires 2 revolutions? Is it because the real track isn't the black coin but the trace of the circle's center when moving (which equals 4[pi])?
It makes me feel uneasy... Can anyone give a satisfactory/intuitive explanation?