MelissaJL
- 50
- 0
Two masses connected by a string uniform circular motion. HELP! :)
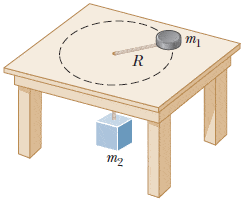
A puck of mass m1 is tied to a string and allowed to revolve in a circle of radius R on a frictionless, horizontal table. The other end of the string passes through a small hole in the center of the table, and an object of mass m2 is tied to it. The suspended object remains in equilibrium while the puck on the tabletop revolves.
What is the tension in the string? (Use any variable or symbol stated above along with the following necessary: g.)
So. I keep looking at this problem...there's more questions to this but the first part is stopping me from completing the others. I was wondering how does the mass m2 effect the tension in the string if it is stationary? I know the tension for mass m1 by itself would simply be T=m1v2/R. Also that if I isolated mass m2 the tension would simply be T=m2g. How do I incorporate them or is one case null? Any suggestions? Thank you :)
Homework Statement
A puck of mass m1 is tied to a string and allowed to revolve in a circle of radius R on a frictionless, horizontal table. The other end of the string passes through a small hole in the center of the table, and an object of mass m2 is tied to it. The suspended object remains in equilibrium while the puck on the tabletop revolves.
What is the tension in the string? (Use any variable or symbol stated above along with the following necessary: g.)
So. I keep looking at this problem...there's more questions to this but the first part is stopping me from completing the others. I was wondering how does the mass m2 effect the tension in the string if it is stationary? I know the tension for mass m1 by itself would simply be T=m1v2/R. Also that if I isolated mass m2 the tension would simply be T=m2g. How do I incorporate them or is one case null? Any suggestions? Thank you :)