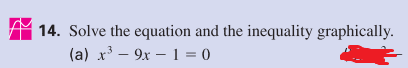Cubic non-linear inequality (HELP)

AI Thread Summary
The discussion centers on understanding a cubic non-linear inequality from a review test. Participants suggest plotting the cubic function and decomposing it to find zeros, which can help in analyzing the inequality across different intervals. It is noted that the function may have up to three zeros, and the direction of the inequality needs to be considered for each interval. The original poster struggles with identifying roots, mentioning that neither +1 nor -1 are roots, and the Rational Root Theorem is not applicable. Cardano's method is recommended as a potential solution for solving the cubic equation.
aew782
Messages
3
Reaction score
0
I just can't figure this out one question from my review test. I don't know hot to express it graphically or algebraically.
VlOaP.png
 
Mathematics news on Phys.org
I don't see any inequality.

As far as expressing the equation graphically, you just plot it.
 
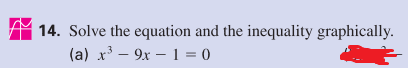
aew782 said:
I just can't figure this out one question from my review test. I don't know hot to express it graphically or algebraically.
VlOaP.png

Try to decompose the cubic expression to find the zeros, meaning find if possible its linear and any quadratic factors (if quadratic factor cannot be factored further). It may have as many as three zeros, but not more. The function (now being equal to zero) is in possibly four intervals. You don't show us the direction of your inequality but you say you want to analyze the inequality; but anyway, you check the quality of the value of the "inequality" for each interval of the x-axis and determine if the x value is true for the inequality or false.

EDIT: harder than I thought. +1 is not a root and -1 is not a root. Rational Root theorem will not work.
 
Last edited:

Thread 'What Exactly is Dirac’s Delta Function? - Insight'

Insights auto threads is broken atm, so I'm manually creating these for new Insight articles. In Dirac’s Principles of Quantum Mechanics published in 1930 he introduced a “convenient notation” he referred to as a “delta function” which he treated as a continuum analog to the discrete Kronecker delta. The Kronecker delta is simply the indexed components of the identity operator in matrix algebra Source: https://www.physicsforums.com/insights/what-exactly-is-diracs-delta-function/ by...
View full post »

Thread 'Non-orthogonal bases'

Suppose ,instead of the usual x,y coordinate system with an I basis vector along the x -axis and a corresponding j basis vector along the y-axis we instead have a different pair of basis vectors ,call them e and f along their respective axes. I have seen that this is an important subject in maths My question is what physical applications does such a model apply to? I am asking here because I have devoted quite a lot of time in the past to understanding convectors and the dual...
View full post »
Thread 'Imaginary Pythagoras'

Thread 'Imaginary Pythagoras'

I posted this in the Lame Math thread, but it's got me thinking. Is there any validity to this? Or is it really just a mathematical trick? Naively, I see that i2 + plus 12 does equal zero2. But does this have a meaning? I know one can treat the imaginary number line as just another axis like the reals, but does that mean this does represent a triangle in the complex plane with a hypotenuse of length zero? Ibix offered a rendering of the diagram using what I assume is matrix* notation...
View full post »

Similar threads

B What Are Basic Questions About Understanding Inequalities?
Replies
12
Views
2K
MHB Solving Cubic Equation: x^3 - kx + (k + 11) = 0
Replies
3
Views
2K
I Violation of Bell Inequality with unentangled photons
2
Replies
73
Views
955
I How to propagate errors through a regression & non-linear model?
Replies
8
Views
2K
A Deriving an inequality from a paper
Replies
6
Views
2K
Restricted (Natural) cubic spline - wrong equation?
Replies
1
Views
2K
MHB Understanding Cubic Equation Formula for Polynomials of Degree Three
Replies
9
Views
3K
Mathematical inequality measures for the social sciences
Replies
12
Views
1K
MHB Why are the cubic roots of 1 expressed as cis 120 degrees?
Replies
4
Views
2K
I Can Non-Linear Functions Be Converted to Linear Systems?
Replies
10
Views
2K

Hot Threads

Recent Insights

Back
Top