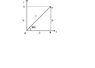avistein
- 48
- 1
I cannot understand what is vector resolution.It is said in the book that ON is the resolved part of A along X axis.It is also known as the x-component of A or the horizontal component of A.Ax may be regarded as the projection of A on X-axis. OM is the the resolved part of A along Y-axis.It is also known as the y-component of A or vertical component of A.The vertical component of A may be regarded as the projection of A on Y-axis.Now what is that projection? Is it the image of A on X-axis or Y axis?
Then why Ax+Ay=A and not A=Ax or A=Ay?If Ax and Ay are the images of A on X and Y resp. then the magnitude of Ax and Ay should be same as A,but no, why? Please explain me.I am very much confused.
Then why Ax+Ay=A and not A=Ax or A=Ay?If Ax and Ay are the images of A on X and Y resp. then the magnitude of Ax and Ay should be same as A,but no, why? Please explain me.I am very much confused.