koii123
- 8
- 0
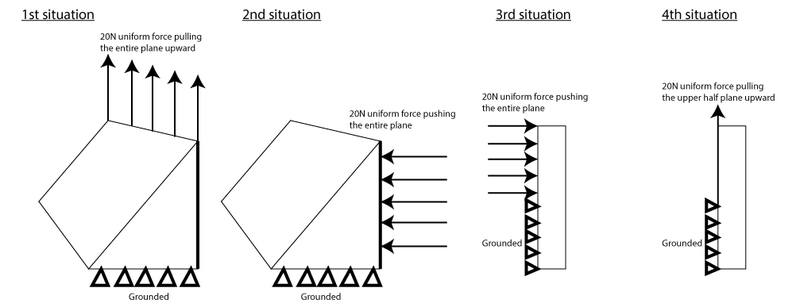
suppose i have 4 solids like this:
and the solid have shear stress and tensile stress 12N/mm2 and 15N/mm2 respectively,
suppose i know the area of each surface,
how can i judge whether this solid is able to withstand 20N load?
what kind of formula should i use?
and the solid have shear stress and tensile stress 12N/mm2 and 15N/mm2 respectively,
suppose i know the area of each surface,
how can i judge whether this solid is able to withstand 20N load?
what kind of formula should i use?