StudentofPhysics
- 65
- 0
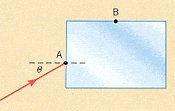
The drawing shows a rectangular block of glass (n = 1.52) surrounded by liquid carbon disulfide (n = 1.63). A ray of light is incident on the glass at point A with a = 46.0° angle of incidence. At what angle of refraction does the ray leave the glass at point B?
I know to use n1 sin 01 = n2 sin 02 (0 = theta)
i came up with 50.48 degrees, which was wrong. Then I figured since it was traveling back out of the block, maybe i should keep going and solve for that angle, which just cam out to be 46 degrees, also wrong.
What am I doing wrong?
I know to use n1 sin 01 = n2 sin 02 (0 = theta)
i came up with 50.48 degrees, which was wrong. Then I figured since it was traveling back out of the block, maybe i should keep going and solve for that angle, which just cam out to be 46 degrees, also wrong.
What am I doing wrong?