Electric Field due to a line of charge

stunner5000pt

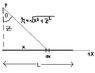
Have a look at the diagram

Find the elctric field a distance z above one end of a astraight line segment of lenght L which carries uniform line charge lambda. Check that your formula is consistent with what you would expect for the case z >> L

SOlution:
[tex] \lambda= q/L [/tex]
[tex] dq = \lambda dx [/tex]

For the electric Field in the horizontal (points to the left and is negative)

[tex] dE_{x} = \frac{1}{4 \pi \epsilon_{0}} \frac{dq}{(z^2 + x^2)} \sin \theta [/tex]

Subsituting what we know about sin theta and dq

[tex] dE_{x} = \frac{1}{4 \pi \epsilon_{0}} \frac{\lambda dx}{(z^2 + x^2)} \frac{x}{\sqrt{z^2 + x^2}} [/tex]

integrating x = 0 to x = L

[tex] E_{x} = \int dE_{x} = \frac{\lambda}{4 \pi \epsilon_{0}} \int_{x=0}^{x=L} \frac{xdx}{(z^2+x^2)^{\frac{3}{2}}} = \frac{\lambda}{4 \pi \epsilon_{0}} \left[ \frac{-1}{\sqrt{z^2 + x^2}} \right]_{x=0}^{x=L} = \frac{\lambda}{4 \pi \epsilon_{0}} \left[ \frac{-1}{\sqrt{z^2 + L^2}} + \frac{1}{z} \right] [/tex]

[tex] E_{x} = \frac{\lambda}{4 \pi \epsilon_{0}} \left[ \frac{1}{z} -\frac{1}{\sqrt{z^2 + L^2}} \right] [/tex]

ok so suppose z >> L then the electric field is zero?? Shouldnt it reduce to that of a point charge and not zero?? this should be regardless of whether i solve for x or z right??

for the Z direction i got
[tex] E_{z} = \frac{\lambda}{4 \pi \epsilon_{0}z} \frac{L}{\sqrt{L^2 + z^2}} [/tex]
unlike the last one this one does reduce to the equatiopn for a point charge but is off my a factor of 1/z ...

combining the two yields

[tex] \vec{E} = \frac{\lambda}{4 \pi \epsilon_{0}} \left[ \frac{1}{z} -\frac{1}{\sqrt{z^2 + L^2}} \right] \hat{x} + \frac{\lambda}{4 \pi \epsilon_{0}z} \frac{L}{\sqrt{L^2 + z^2}} \hat{z} [/tex]


is there soemthing wrong with the calculationg ofr hte X Horizontal Direction?? Please help

Thank you in advance for your help and advice!

Attached Thumbnails

 

Doc Al

If you get far enough away, the field from anything (finite) goes to zero! But you need to understand how it approaches zero. In this case, think about it: You are very far from a point charge--What's the direction of the field?

It's not off. You just need to examine its behavior as z goes to infinity. Use a binomial expansion:
[tex](L^2 + z^2)^{-1/2} \approx (1/z)(1 - \frac{L^2}{2z^2})[/tex]

Peppe

I'm studying from Griffiths too :) and i've a question about this exercize.

The electric potential:

[tex]V = \frac{ \lambda }{4\epsilon_0 \pi} ln\left(\frac{L+\sqrt{z^2+L^2}}{z}\right) [/tex]


Calculating the electric field from the V's gradient, it has x component always at zero.
Where the problem?

I'm sorry for my poor english, good evening mate!

lepton5

Yeah, Griffith's book is good.

From your calculation for [tex]\vec{E}[/tex] (yes i think it's correct for both direction), for z >> L, the electric field of component - x will dissapear (since [tex]\frac{1}{z} - \frac{1}{z} = 0)[/tex] and leaves for us the z - component as below:


after simplifying, [tex]\vec{E} = \frac{\lambda L}{4 \pi \epsilon_{0}z^2}\hat{z}[/tex] for z>>L.


the case is the same as above example from griffith's book (that is for E at a distance z above midpoint of line L). I quoted it : From far away the line

"looks" like a point charge [tex]q = 2\lambda L[/tex].

I think x and y component will be gone since you do grad [tex]\nabla[/tex]-operation to potential (the potential only depend on z). so,

[tex]\vec{E} = -\nabla V = -\frac{\lambda}{4\pi \epsilon_{0}}\frac{\partial}{\partial z}\ln (\frac{L + \sqrt{z^2 + L^2}}{z})[/tex].

suppose [tex]k = \sqrt{z^2 + L^2}[/tex],


it will give [tex]\vec{E} = \frac{\lambda}{4 \pi \epsilon_{0}}(\frac{z}{k(L + k)} - \frac{1}{z})\hat{z}[/tex]


btw, i cant find this problem in griffith's book....