pcandrepair
- 65
- 0
[SOLVED] E-field at the center of a semicircle
Calculate E at center of semicircle:
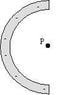
A uniformly charged insulating rod of length L = 12 cm is bent into the shape of a semicircle as shown. The rod has a total charge of Q = -6 nC. Find the magnitude of the electric field at the point P -- the center of the semicircle. (Answer in units of N/C.)
E = K((Q)/(r^2))
To find the distance/radius from the point P to any point on the semicircle would be...
12cm*2 = circumference
2*pi*r = 24cm
r = 3.8197cm or .038197m
When I use the equation under the "relevant equations" heading, I'm getting a really huge (E) of about 36,970 N. This can't be right and I'm not sure of where to go from here. Any help would be greatly appreciated. Thanks!
Homework Statement
Calculate E at center of semicircle:
A uniformly charged insulating rod of length L = 12 cm is bent into the shape of a semicircle as shown. The rod has a total charge of Q = -6 nC. Find the magnitude of the electric field at the point P -- the center of the semicircle. (Answer in units of N/C.)
Homework Equations
E = K((Q)/(r^2))
The Attempt at a Solution
To find the distance/radius from the point P to any point on the semicircle would be...
12cm*2 = circumference
2*pi*r = 24cm
r = 3.8197cm or .038197m
When I use the equation under the "relevant equations" heading, I'm getting a really huge (E) of about 36,970 N. This can't be right and I'm not sure of where to go from here. Any help would be greatly appreciated. Thanks!