myr10
- 2
- 0
Homework Statement
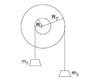
Two pulley wheels, or respective radii R1 =
0.34 m and R2 = 0.64 m are mounted rigidly
on a common axle and clamped together. The
combined moment of inertia of the two wheels
is I + 1.2 kg*m^2.
Mass m1 = 25 kg is attached to a cord
wrapped around the first wheel, and another
mass m2 = 19 kg is attached to another cord
wrapped around the second wheel.
The acceleration of gravity is 9.8 m/s^2 :
Find the angular acceleration of the system.
Take clockwise direction as positive. Answer
in units of rad/s^2.
Homework Equations
The Attempt at a Solution
im not sure how to go about solving this.