Ericv_91
- 25
- 1
Homework Statement
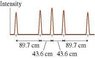
The figure shows the interference pattern on a screen 1.0 m behind a diffraction grating. The wavelength of the light is 600 nm. How many lines per millimeter does the grating have?
Homework Equations
lines/mm = 1/ distance between slits
The Attempt at a Solution
Quite frankly I don't have a clue how to solve this. I know that the number of lines per millimeter is equal to the inverse of the distance between slits, but what happens if there are more than 2 slits of different distances from each other? I took a shot in the dark and tried to add up the reciprocals of all the distances, but that proved to be incorrect because it gave me a very small number around 0.006. Does anyone have any helpful suggestions?