Linus Pauling
- 187
- 0
1. Five equal-mass particles (A–E) enter a region of uniform magnetic field directed into the page. They follow the trajectories illustrated in the figure.
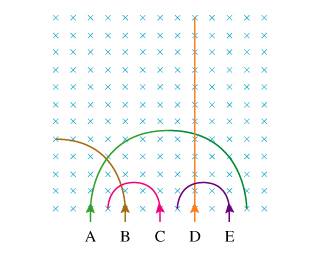
Rank from largest to smallest velocity
2. qvBsin(theta) = ma
qvB = ma = m(v^2/r)
v = qBr/m
3. Based on their radii, it should be A > B > C=E
But what about D? It is neutral, so has no radius because it doesn't go in a circle, but clearly has a velocity despite r = 0. Is the answer indeterminate, then?
Rank from largest to smallest velocity
2. qvBsin(theta) = ma
qvB = ma = m(v^2/r)
v = qBr/m
3. Based on their radii, it should be A > B > C=E
But what about D? It is neutral, so has no radius because it doesn't go in a circle, but clearly has a velocity despite r = 0. Is the answer indeterminate, then?