Deathfish
- 80
- 0
1. 1. Homework Statement
Ok. I'm given a force diagram, and I have to figure out the reaction forces at the two points on the ground.
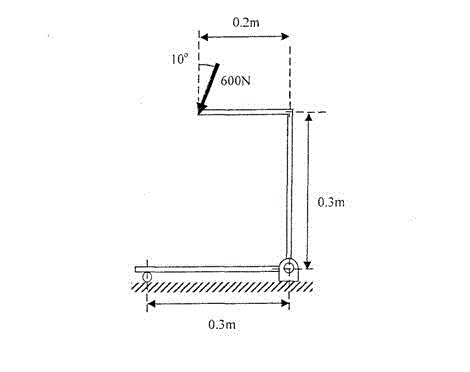
answer key: (498.1N↑; 104.2N→, 92.8N↑)
Ok. I only got so far as the x-reaction force at the pivot... 600 sin 10 = <- 104.2N
Total y-reaction forces - 600 cos 10 = 590.88N
600 cos 10 = 590.88N
600 sin 10 = 104.2N
root 0.2^2 x 0.3^2 = 0.36m
104.19N x 0.3m = 31.257Nm
590.88N x 0.2m = 118.177 Nm
498.1N + 92.8N = 590.9N
i can't figure out how to get 498.1N and 92.8N at the two points respectively...
anyone can show how to achieve the answer? Thx
Ok. I'm given a force diagram, and I have to figure out the reaction forces at the two points on the ground.
answer key: (498.1N↑; 104.2N→, 92.8N↑)
Homework Equations
Ok. I only got so far as the x-reaction force at the pivot... 600 sin 10 = <- 104.2N
The Attempt at a Solution
Total y-reaction forces - 600 cos 10 = 590.88N
600 cos 10 = 590.88N
600 sin 10 = 104.2N
root 0.2^2 x 0.3^2 = 0.36m
104.19N x 0.3m = 31.257Nm
590.88N x 0.2m = 118.177 Nm
498.1N + 92.8N = 590.9N
i can't figure out how to get 498.1N and 92.8N at the two points respectively...
anyone can show how to achieve the answer? Thx