Analyzing Forces in Structures: West-Point Bridge Designer

  • Thread starter Thread starter phrontist
  • Start date Start date
  • Tags Tags
    Forces Structure
AI Thread Summary
The discussion focuses on analyzing forces in structures using the West-Point Bridge Designer. Participants emphasize the importance of defining the support conditions of the structure before proceeding with force analysis. The initial query highlights uncertainty about calculating forces in a simple triangular structure. Clarifying support mechanisms is crucial, as they influence the force reactions and overall analysis. Understanding these foundational elements is essential for accurate calculations in structural engineering.
phrontist
Messages
5
Reaction score
0
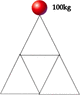
I've been toying around with West-Point Bridge Designer and wondering how it does it's calculations. If you have a simple structure like the image below, how do you analyze the forces on each member (assume all triangles are equilangular and equilateral)? I'd imagine it's all vectors, but I'm not sure about anything beyond that. Could someone link me in the right direction, or diagram the forces?
 

Attachments

  • structure.gif
    structure.gif
    5.1 KB · Views: 557
Last edited:
Physics news on Phys.org
First of all you have to define how the structure is supported. Your drawing does not show any support. Is the structure flying in the space?. When you clear how is supported I will give you some hints for the resolution, because it depends on the structure force reactions.
 
Thread 'Gauss' law seems to imply instantaneous electric field'

Thread 'Gauss' law seems to imply instantaneous electric field'

Imagine a charged sphere at the origin connected through an open switch to a vertical grounded wire. We wish to find an expression for the horizontal component of the electric field at a distance ##\mathbf{r}## from the sphere as it discharges. By using the Lorenz gauge condition: $$\nabla \cdot \mathbf{A} + \frac{1}{c^2}\frac{\partial \phi}{\partial t}=0\tag{1}$$ we find the following retarded solutions to the Maxwell equations If we assume that...
View full post »

Thread 'Do electron density waves accompany EM waves in coaxial cables?'

Maxwell’s equations imply the following wave equation for the electric field $$\nabla^2\mathbf{E}-\frac{1}{c^2}\frac{\partial^2\mathbf{E}}{\partial t^2} = \frac{1}{\varepsilon_0}\nabla\rho+\mu_0\frac{\partial\mathbf J}{\partial t}.\tag{1}$$ I wonder if eqn.##(1)## can be split into the following transverse part $$\nabla^2\mathbf{E}_T-\frac{1}{c^2}\frac{\partial^2\mathbf{E}_T}{\partial t^2} = \mu_0\frac{\partial\mathbf{J}_T}{\partial t}\tag{2}$$ and longitudinal part...
View full post »

Similar threads

I On whether the motion of a Foucault pendulum bob is comparable to ballistics
Replies
10
Views
2K
I Could Physically Slamming on a Table Damage the Home Floor/Structure?
Replies
9
Views
2K
A Principle of Virtual Work and the forces that DO NOT do work
Replies
4
Views
2K
I Calculate the Resultant Force Between 4 Points
Replies
3
Views
2K
What Are Fictitious Forces and How Do They Affect Falling Objects?
Replies
4
Views
2K
Analyzing a Complex Structure for Statics Project
Replies
4
Views
2K
Need help with balsa tower design
Replies
3
Views
2K
Engineering How should an H bridge circuit be analyzed?
Replies
5
Views
3K
I What are the effects of Buoyancy & G-force combined in this scenario?
Replies
9
Views
2K
B Electric Flux - confused about integrating over a tilted area
Replies
8
Views
2K

Hot Threads

Recent Insights

Back
Top