Writing Gravitation Force On Central Sphere In Unit Vector Notation

[GingerBread27]

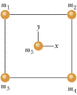
In Figure 13-34, a square of edge length 21.0 cm is formed by four spheres of masses m1 = 6.00 g, m2 = 3.00 g, m3 = 1.00 g, and m4 = 6.00 g. In unit-vector notation, what is the net gravitational force from them on a central sphere with mass m5 = 2.40 g?

Well by using Newton's Law of Gravitation I get a single answer and I know it points towards m2 (or maybe I'm wrong). I just don't know how to write this in unit-vector notation.

I did F={(6.67e-11 m^3/kg*s^2)(.0024kg)(.003kg-.001kg)}/{(.148m)^2}

I get F=1.46e-14 N. I don't know if this is right, and if it is right I don't know how to put it in unit-vector notation.

Nevermind figured it out :)

 

[sizzler]

Did you multiply by sin45/cos45 to get
F = <1.034E-14, 1.034E-14> ?
I was having the same difficultly...

 

[wais]

In unit-vector notation, the net gravitational force on the central sphere with mass m5 = 2.40 g would be represented as:

F = 1.46e-14 N * (0.707i + 0.707j)

Where i and j are unit vectors in the x and y directions, respectively. This represents the direction of the force, which, as you correctly calculated, points towards the m2 sphere. The magnitude of the force is given by the scalar value, 1.46e-14 N.