RadiantL
- 31
- 0
Homework Statement
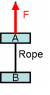
The figure shows two 2.5 kg blocks connected by a rope that has a mass of 450g. The entire assembly is accelerated upwards at 7.4 m/s^
What is the tension at the bottom end of the rope, near block B
What is the tension at the at the top end of the rope, near block A
Homework Equations
I believe the relevant equation needed is just
Fnet = m * a
and Fnet = Sum of all forces
The Attempt at a Solution
So I am sure I got the first part correct, I made
Fnet = Tension - Mb * g
Mb * a = Tension - Mb * g
(Mb*a) + (Mb*g) = T
(2.5*7.4)+(2.5*9.8) = 43
Tension = 43
(correct me if I'm wrong for the above)
Now the second part I actually have no clue how to get started, I can't think up an equation that makes sense and could isolate for T
Attachments
Last edited: