Calculating Electric Force: 2 Electrons & a Proton

[Mdhiggenz]

Homework Statement

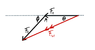
Take a look at this image first

If two electrons are each 2.50×10−10 from a proton, as shown in the figure, find the magnitude and of the net electrical force they will exert on the proton.

Homework Equations

The Attempt at a Solution

k=1/4πε0

So what I did first was calculate the Electric Force in the x directon



Fx= (k*q^2/r^2)cos(theta)

Fy=( k*q^2/r^2)sin(theta)

Then took the magnitude of the sum √(x)^2+(y)^2

And thought that would give me the answer for part one, where did I go wrong?

 

[Simon Bridge]

You seem to have left off the cotribution
The force on the proton is the sum of the forces due to the two electrons.
$$F=\frac{ke^2}{r^2}$$ ... for each electron - but the directions are different.
You also need to show the correct direction for the resultant force.

 

[Mdhiggenz]

I don't quite understand? Wouldn't me getting the cos / sin be me taking the directions into consideration?

 

[Saitama]

I don't quite understand? Wouldn't me getting the cos / sin be me taking the directions into consideration?

I would suggest you not to find the force in a particular direction. Keep everything in variables. Each electron would exert an equal force in magnitude, say F. The resultant force will be \sqrt{F^2+F^2+2F^2cosθ}, where θ=65 degrees. Solve the expression, get it into its simplest form i.e factor out F. Plug in the values.

 

[Mdhiggenz]

I got the correct answer using your method, but I don't quite understand how you got that.

It would make sense to me if it was √F^2sin∅+F^2cos

But not the √F^2+f^2+2f^2cos∅

can you elaborate on how you achieved that formula?

Thanks

 

[Saitama]

I got the correct answer using your method, but I don't quite understand how you got that.

It would make sense to me if it was √F^2sin∅+F^2cos

But not the √F^2+f^2+2f^2cos∅

can you elaborate on how you achieved that formula?

Thanks

That's the formula for finding resultant of two vectors. Don't you know about it?

 

[Mdhiggenz]

Nope never knew about it but I do now (: is it always cos and never sine?

 

[Saitama]

Nope never knew about it but I do now (: is it always cos and never sine?

Yes, it is always cosθ. You should check this out from any physics textbook you have. It should be there in a chapter about "Vectors".

 

[Simon Bridge]

I hate to direct people to memorize equations - the formula is a special case of the cosine rule for a scalene triangle.

To add two vectors, draw them head-to-tail (you should have seen this before) ... the resultant goes from the tail of the first one to the head of the second one. This gives you a triangle. Draw it out and you'll see.

You can also use the sine rule for the same triangle in this case because, since it is an isosceles triangle you know all the interior angles. But this is not generally true.

 

[Simon Bridge]

I couldn't find a vector-add diagram online that had all the elements I wanted ... so I drew my own:

... in the above, we want to do $\vec{F}_{tot}=\vec{F}_A+\vec{F}_B$ - magnitudes and directions are shown in the diagram.

We place the vectors head-to-tail.
In general $F_A \neq F_B$:

The cosine rule says that: $$F_{tot}^2 = F_A^2+F_B^2-2F_AF_B\cos(A)$$... notice that $A=180-\phi$ (in degrees) and use the identity: $\cos(180-\phi)=-\cos(\phi)$ to get: $$F_{tot}^2 = F_A^2+F_B^2+2F_AF_B\cos(\phi)$$
Once you've got $F_{tot}$ you can use the sine rule to find $\theta$ - the direction of the resultant. $$\frac{F_{tot}}{\sin(A)} = \frac{F_B}{\sin(\theta)} = \frac{F_A}{\sin(180-A-\theta)}$$

This is not normally any more convenient that working with components ... unless...

In the special case where $F_A=F_B=F$ then $\theta = \phi/2$ and the rule becomes: $$F_{tot}^2 = 2F^2\big ( 1+\cos{\phi} \big )$$ ... which can simplify things a great deal.

In general - learn the sine and cosine rules rather than these vector ones, and get used to drawing the diagrams to guide your thinking.

 

[Saitama]

Nice explanation and nice diagram, Simon Bridge!

 

[Simon Bridge]

I was concerned that different countries do things differently: in NZ (and afaik in UK and USA) it is usual for beginning students to go from head-to-tail adding to components without seeing the cosine and sine rules (which will be in a more advanced math course). OP may not be taught from a textbook - and there is no guarantee the textbook will have these relations.

Even with what I did above - they are still mysterious rules that need their own derivation ... which OP will have to look up.

Using components - defining the -x axis as the direction of F_A we would write:
$$\vec{F}_A = -F_A\hat{\imath}$$ $$\vec{F}_B=-F_B\cos{\phi}\hat{\imath}-F_B\sin(\phi)\hat{\jmath}$$... then I can do: $$\vec{F}_{tot}=\big (-F_A-F_B\cos{\phi}\big ) \hat{\imath}-F_B\sin(\phi)\hat{\jmath}$$

Then it is a matter of applying Pythagoras to get the total.
It is usually felt that this method is easier for beginners. OP's mistake was leaving one of the forces out.