PirateFan308
- 91
- 0
Homework Statement
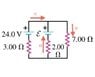
What must the emf ε in the figure be in order for the current through the 7.00 ohm resistor to be 1.75A? Each emf source has negligible internal resistance.
Homework Equations
Kirchhoff's Rule:
\sum I=0 junction rule
\sum V=0 loop rule
The Attempt at a Solution
I have drawn my current directions as shown in the attachment below.
By the junction rule, I know that I_2 = I_3+I_1 and it is given that I_2=1.75A.
I drew a loop clockwise around the entire thing and came up with the following equation:
24V-(7 ohm)(1.75A)-(I_1)(3 ohm) = 0
so that I have
I_1 = (24V-12.25V)/3= 3.92A
and then
I_3 = I_2 - I_1 = 2.17
Drawing loop 2 clockwise within the right inner loop I have the following equation:
-(7 ohm)(I_2) - (I_3)(2 ohm) + ε = 0
solving for ε, I get
ε = (12.25V)+(4.34V) = 16.59V
Also, if I draw a clockwise loop inside the right inner loop, I have the following equation:
-ε + (I_3)(2 ohm) - (I_1)(3 ohm) + 24 V = 0
which simplifies to
ε = 16.58V
I can find no mistakes (and I have checked over my work a few times) but it is the wrong answer. Could anyone please help me? Thanks!