anelephant09
- 3
- 0
Hi all,
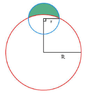
Find the area of the crescent-shaped region (called a lune) bounded by arcs of circles with radii r and R.
http://mathhelpforum.com/attachments/calculus/19696-find-area-untitled.png
I know we have to use arcsin which is $$ \frac {1}{\sqrt{a^{2}-x^{2}}}$$
I tried plotting the circles on a coordinate axis with the bigger circle centered at the origin and the smaller circle centered at a point (0,b) but I am not really sure where to go from here... If this was geometry, it would have been easy, but we have to use calc on this problem.
So far, i started with $$r \sqrt{R^{2}-r^{2}} +\frac{pir^{2}}{2}$$
but I am stuck now. Can anyone provide a push in the right direction for me?
Thanks in advance.
Homework Statement
Find the area of the crescent-shaped region (called a lune) bounded by arcs of circles with radii r and R.
http://mathhelpforum.com/attachments/calculus/19696-find-area-untitled.png
Homework Equations
I know we have to use arcsin which is $$ \frac {1}{\sqrt{a^{2}-x^{2}}}$$
The Attempt at a Solution
I tried plotting the circles on a coordinate axis with the bigger circle centered at the origin and the smaller circle centered at a point (0,b) but I am not really sure where to go from here... If this was geometry, it would have been easy, but we have to use calc on this problem.
So far, i started with $$r \sqrt{R^{2}-r^{2}} +\frac{pir^{2}}{2}$$
but I am stuck now. Can anyone provide a push in the right direction for me?
Thanks in advance.