Find Max Power Dissipation in Circuits with Variables

[stunner5000pt]

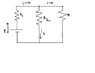
In the circuit, E, R1 and R2 have constant values. However R has a variable value. FInd an epxression for R that results in the max power dissipation in that resistor.
so do i do this
$$i_{1} = i + i_{2}$$
$$E - i_{1} R_{1} - i_{2} R_{2} = 0$$
$$E - i_{1} R_{1} - iR = 0$$
$$i_{2} R_{2} - iR = 0$$
not too sure about the last one...
and the power dissipation in that resitor is given by $$P = i^2 R$$ But to find the max power dissipation do i plug that expression for i back into the above expression and then differentiate OR sub i into this
$$\frac{dP}{dR} = 2iR + i^2$$
i used a sample value for i and got different values for the derivative. Which is correct?
Please help!

 

[BobG]

You should use your Thevenin equivalent and Norton equivalent for this one - unless they're making you do this using differentiation and limits at least once just to make sure you truly appreciate Thevenin and Norton equivalents.