Laplace equation Definition and 154 Threads
-
G
Undergrad Boundary conditions for a stream function in a hydrodynamics problem
The situation is like this: we have a bath of a square cross-section. The cross-section is modeled by an area ##\{x, y: 0\leq x\leq 1, 0\leq y\leq 1\}## in 2d Cartesian coordinates (the gravity fied direction is opposite to the y-axis). There is a hole in the floor of the bath, it starts at... -
H
Heat transfer: Temperature distribution inside a sphere submerged in a fluid
Consider a sphere of thermal diffusivity ##\kappa_2## is submerged in an incompressible and stationary fluid of thermal diffusivity ##\kappa_1##. The fluid is held between 2 large plates ( at T_0 for the top plate and T_1 for the bottom plate). What is the stationary temperature distribution...- happyparticle
- Thread
- Heat conduction Hydrodynamic Laplace equation
- Replies: 13
- Forum: Advanced Physics Homework Help
-
H
Potential function of a flow around a stagnation point
To find the potential function, I'm starting with the laplace equation ##\Delta \phi = 0 ## In cartesian coordinates the solution is ##\phi = \sum_m (A_m e^{mx} + B_m e^{-mx}) (C_m sin(my) + D_m cos (my))## Using the first boundary condition. ## u = \Delta \phi = -u_0 \hat{y}## The gradient in...- happyparticle
- Thread
- Fluid dynamic Laplace equation
- Replies: 19
- Forum: Advanced Physics Homework Help
-

Undergrad Dirichlet problem boundary conditions
The Dirichlet problem asks for the solution of Poisson or Laplace equation in an open region ##S## of ##\mathbb R^n## with a condition on the boundary ##\partial_S##. In particular the solution function ##f()## is required to be two-times differentiable in the interior region ##S## and...- cianfa72
- Thread
- Boundary conditions Boundary value problem closure Laplace equation Subspaces
- Replies: 4
- Forum: Differential Geometry
-

Potential in the three regions of an infinite slab
for the boundary conditions for this problem I understand that Electric field and Electric potential will be continuous on the boundaries. I also know that I can set the reference point for Electric potential, wherever it is convenient. This gives me the fifth boundary condition. I am confused...- workhorse123
- Thread
- Boundary condition Laplace equation Partial derivative
- Replies: 1
- Forum: Advanced Physics Homework Help
-
H
Graduate How was this infinite sequence of numbers found? (non-commutative geometry )
Hi Pfs, I read these slides: https://indico.math.cnrs.fr/event/782/attachments/1851/1997/Connes.pdf It is about non commutative geometry (Alain Connes) After Shapes II, you see a the plots of the square roots of a sequence of numbers given below: 5/4, 2, 5/2, 13/4 .... I think that they are the...- Heidi
- Thread
- Laplace equation
- Replies: 4
- Forum: Beyond the Standard Models
-
T
Graduate General solution to Laplacian in cylindrical coordinates
I am trying to model the voltage function for a very long cylinder with an assigned surface charge density or voltage. Then the solution inside the cylinder is: $$\sum_{n=0}^{\infty}A_n r^n cos(nθ)$$ And$$\sum_{n=0}^{\infty}A_n r^-n cos(nθ)$$ outside. Is that correct- Trollfaz
- Thread
- Cylindrical coordinates Laplace equation
- Replies: 13
- Forum: Electromagnetism
-
H
Find equilibrium profile T(x) Between Two Rods
Knowing that we are in equilibrium ##\frac{\partial}{\partial t} = 0##. We now have a Laplace's equation ##\kappa \frac{\partial^2 T}{\partial x^2} = 0## I separated the rod in 2 halves. The solution of this equation is ##\kappa_1 \frac{\partial2 T}{\partial x2} = C_1## Integrating both side...- happyparticle
- Thread
- Heat diffusion Laplace equation
- Replies: 7
- Forum: Advanced Physics Homework Help
-
H
How to Solve the Laplace Equation for Potential Flow Around a Sphere?
I tried to find a solution to the Laplace equation using spherical coordinates and the separable variable method. However, I found equations that I simply don't know how to find a solution. Thus, I tried in cylindrical coordinates with an invariance in ##\theta## but now I'm facing this...- happyparticle
- Thread
- Fluid Laplace equation
- Replies: 1
- Forum: Advanced Physics Homework Help
-
Y
Graduate Electric field vs coupling between transmission lines
Hello All, I'm trying to create equation which can describe relation between electric fields of three coupled-lines and coupling between them. Let we say that, we have thee lines having infinit length which are placed above ground plane in distance h. The distance between coupled lines is...- Young_Scientist23
- Thread
- Electric field Laplace equation
- Replies: 12
- Forum: Electromagnetism
-

Undergrad Question regarding Laplace's Equation for regions with charges
Why doesn't the **Laplace's equation**(#\nabla^2V=0#) hold in the region within the sphere when there is a charge inside it ? Is it because #ρ \ne 0# within the sphere and it becomes a **poisson equation**($\nabla^2V=\dfrac{-ρ}{ε_0}$) and changes the characteristics of **Harmonic Solution**...- Harikesh_33
- Thread
- Charges Electro static Laplace equation Laplace's equation
- Replies: 11
- Forum: Electromagnetism
-
P
Undergrad Laplace equation with irregular boundaries
Is there a way to solve Laplace’s Equation on irregular domains if the domain’s shape is given by a function for example a 2D parabolic plate. I keep seeing numerical methods but I want to know is there an ANALYTICAL method to solve it on an irregular domain. If there isn't are there approximate...- physwiz222
- Thread
- Laplace Laplace equation
- Replies: 4
- Forum: Beyond the Standard Models
-

Undergrad Laplace's equation in presence of a dipole (perfect or physical)
Does Laplace's equation hold true for electrostatic potential at the location of a dipole? Or should poisson's equation be used?- Ahmed1029
- Thread
- Dipole Electric dipole Electrostatic potential Laplace equation Laplace's equation Physical
- Replies: 7
- Forum: Electromagnetism
-
C
Undergrad Where to find this uniqueness theorem of electrostatics?
There is a nice uniqueness theorem of electrostatics, which I have found only after googling hours, and deep inside some academic site, in the lecture notes of Dr Vadim Kaplunovsky: Notice that the important thing here is that only the NET charges on the conductors are specified, not their...- coquelicot
- Thread
- Electro static Electrostatic Electrostatic charges Electrostatics Laplace equation Poisson equation Theorem Uniqueness Uniqueness theorem
- Replies: 27
- Forum: Electromagnetism
-

Capacitance of infinitely long coaxial cylinders of elliptical section
I've been able to prove the following inequality $$\frac{2\pi\epsilon_0}{\log\left(\frac{b_1b_2}{a_1^2}\right)}\leq C \leq \frac{2\pi\epsilon_0}{\log\left(\frac{a_1a_2}{b_1^2}\right)}$$ but have no clue how to obtain exact value. Can someone check whether this inequality is correct and show how...- Rlwe
- Thread
- Capacitance Coaxial Cylinders Elecrostatics Laplace equation Section
- Replies: 5
- Forum: Advanced Physics Homework Help
-
L
Is the Fourier Transform Correctly Applied in Solving This Laplace Equation?
I have tried to Fourier transform in ##x## and get the result in the transformed coordinates, please check my result: $$ \tilde{u}(k, y) = \frac{1-e^{-ik}}{ik}e^{-ky} $$ However, I'm having some problems with the inverse transform: $$ \frac{1}{2\pi}\int_{-\infty}^\infty...- lriuui0x0
- Thread
- Fourier Fourier transform Laplace Laplace equation Partial differential equations Transform
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
J
Using the Frobenius method on a 2D Laplace
- jkthejetplane
- Thread
- 2d Differential eqautions Frobenius Laplace Laplace equation Method
- Replies: 6
- Forum: Advanced Physics Homework Help
-

Laplace Equation Numerical Solution
I wonder how to incorporate point charge?- jawad hussain
- Thread
- Laplace Laplace equation Numerical
- Replies: 1
- Forum: Advanced Physics Homework Help
-
G
Graduate Laplace eq. in cylindrical coordinates and boundary conditions
- giulianinimat
- Thread
- Bessel function Boundary Boundary conditions Conditions Coordinates Cylindrical Cylindrical coordinates Electric potential Laplace Laplace equation
- Replies: 2
- Forum: Differential Equations
-
D
Radial solutions to the Laplace equation
Part 1 $$\Delta u(x)=\Delta v(|x|)$$ Substitute $$|x|=r=\sqrt{\sum_{i=1}^n{x^2_i}}$$ $$u'(x)= v'(r)\frac{\sum_{i=1}^nx_i}{\sqrt{\sum_{i=1}^n{x^2_i}}}$$ $$u''(x)=v''(r)\frac{\sum_{i=1}^nx_i}{\sqrt{\sum_{i=1}^n{x^2_i}}}+v'(r)f(x)=v''(r)+v'(r)f(x)$$...- docnet
- Thread
- Laplace Laplace equation Radial
- Replies: 12
- Forum: Calculus and Beyond Homework Help
-
Z
Python Tackling Boundary Conditions in Python (Griffins Example)
How to run a numerical simulation of Laplace equation if one of the boundary condition is like this: $$V(x,y) = 0 \text{ when } x \to \infty$$ I am trying to use Python to plot the solution of this Example 3.5. in Griffins EM- zhuang382
- Thread
- Boundary Boundary conditions Conditions Example Finite difference method Laplace equation Python
- Replies: 1
- Forum: Programming and Computer Science
-
F
Show that the real part of a certain complex function is harmonic
Hello, I have to prove that the complex valued function $$f(z) = Re\big(\frac{\cos z}{\exp{z}}\big) $$ is harmonic on the whole complex plane. This exercice immediately follows a chapter on the extension of the usual functions (trigonometric and the exponential) to the complex plane, so I tend...- fatpotato
- Thread
- Complex Complex analysis Complex function Function Harmonic Laplace equation
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
K
What Causes Bubble Oscillation According to Gauss's Law?
From Gauss's Law give ##E=\dfrac{\sigma}{2\epsilon_0}## ##\therefore P_e=\dfrac{\sigma^2}{2\epsilon_0}## Consider at equilibrium (before bubble being charged) ##P_i=P_0+\dfrac{4S}{R}## Using Newton's 2nd Law ##\Sigma F=m\ddot{R}## Let ##R+\delta R## be the new radius Give (after binomial...- kenth
- Thread
- Bubble Charged Gauss's law Laplace equation Oscillation
- Replies: 1
- Forum: Advanced Physics Homework Help
-

How Are Stress Lines and Streamlines Related in Physical Models?
I was initially curious by the fact that streamlines around a circle appear the same as the lines of stress around a hole: I understand that streamlines are the contour lines of the stream function ##\psi## which satisfies the Laplace equation. I was wondering there is a related function for...- person123
- Thread
- Laplace equation Lines Material Stress
- Replies: 14
- Forum: Mechanical Engineering
-
L
Engineering Help with Homework: Solving a Math Formula
i want to ask about my homework im not understand what to do with this formula :- Lucky Pradana
- Thread
- Formula Homework Laplace Laplace equation
- Replies: 3
- Forum: Engineering and Comp Sci Homework Help
-
C
Graduate Electrical potential of a thin wire in an E field
Assume that an infinite metallic plate A lies in the xy-plane, and another infinite metallic plate B is parallel to A and at height z = h. The potential of plate A is 0, and the potential of plate B is constant and equal to V. So, there is a uniform electrostatic field E between plates A and B...- coquelicot
- Thread
- Elecrostatics Electric charge Electrical Electrical potential Field Laplace equation Potential Wire
- Replies: 11
- Forum: Electromagnetism
-

Potential from point charge at distance ##l## from conducting sphere
After looking around a bit, I found that, considering the polar axis to be along the direction of the point charge as suggested by the exercise, the following Legendre polynomial expansion is true: $$\begin{equation}\frac{1}{|\mathbf{r} - \mathbf{r'}|} = \sum_{n=0}^\infty...- migueldbg
- Thread
- Charge Conducting Conducting sphere Eletromagnetism Laplace equation Legendre polynomials Point Point charge Potential Sphere
- Replies: 3
- Forum: Advanced Physics Homework Help
-
F
Undergrad Separation of Variables (PDE) for the Laplace Equation
- FAS1998
- Thread
- Laplace Laplace equation Pde Separation Separation of variables Variables
- Replies: 3
- Forum: Differential Equations
-

Graduate Simple electric potential and Laplace equation
Imagine to be in 2 dimensions and you have to find the potential generated by 4 point-charges of equal charge located at the four corners of a square. To do that I think we simply add all the contributions of each single charge: $$V_i(x, y) = - \frac k {| \mathbf r - \mathbf r_i|}$$ $$ V(x, y)...- dRic2
- Thread
- Electric Electric potential Laplace Laplace equation Potential
- Replies: 8
- Forum: Electromagnetism
-

Visualizing & Solving a 2D Laplace Eq problem (Polar Coordinates)
- majormuss
- Thread
- 2d Coordinates Electrodyanmics Laplace Laplace equation Polar coordinates Separation of variables
- Replies: 2
- Forum: Advanced Physics Homework Help
-

The mean value of the cube, Force Field Laplace equation
Homework Statement I have a value of $$ U=U_0+x (∂U/∂x)+y(∂U/∂y)+z (∂U/∂z)+1/2x^2(∂^2U/∂x^2)+1/2y^(2∂^2U/∂y^2)+...$$ We need to find the mean value of the U. So the answer is $$\overline{\rm U}\approx U_0+a^2/24(∇^2U)$$Homework Equations $$\overline{\rm U}=1/a^3 \int \int\int Udxdydz$$ The...- Arman777
- Thread
- Cube Field Force Laplace Laplace equation Mean Value
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

How can I solve a Laplace equation in a cube with mixed boundary conditions?
Homework Statement There's a metal cunducting cube with edge length ##a##. Three of its walls: ##x=y=z=0## are grounded and the other three walls: ##x=y=z=a## are held at a constant potential ##\phi_{0}## . Find potential inside the cube. Homework Equations The potential must satisfy Laplace...- CptXray
- Thread
- Cube Electrostatics Laplace Laplace equation
- Replies: 10
- Forum: Advanced Physics Homework Help
-
M
Mathematica Solving the Laplace Equation in weird domains
Hi PF! I looked through the documentation on their website, but under the tab "Solve partial differential equations over arbitrarily shaped regions" I am redirected to a page that does not specify how to create a region. Any help is greatly appreciated. Also, if it helps, the domain is a...- member 428835
- Thread
- domains Laplace Laplace equation Weird
- Replies: 1
- Forum: MATLAB, Maple, Mathematica, LaTeX
-

Graduate Solving the Laplace equation over a trapezoidal domain
can anyone help me on how I can map an isosceles trapezoid onto a rectangular/square domain.Actually I need to solve Laplace equation(delta u = 0) over this isosceles trapezoidal domain. Schwarz Christoffel mapping may help me. But can anyone give me any hint on this mapping procedure?- md nabil
- Thread
- Domain Laplace Laplace equation
- Replies: 2
- Forum: Differential Equations
-

MHB Solve Laplace equation on unit disk
Hello! (Wave) I want to solve the Laplace equation on the unit disk, with boundary data $u(\theta)=\cos{\theta}$ on the unit circle $\{ r=1, 0 \leq \theta<2 \pi\}$. I also want to prove that little oscillations of the above boundary data give little oscillations of the corresponding solution of...- evinda
- Thread
- Disk Laplace Laplace equation Unit
- Replies: 33
- Forum: Differential Equations
-
G
A solution to the Laplace equation
Hi, I am looking for the solution to the quadrant problem of the Laplace equation in 2 dimensions with Dirichlet boundary conditions \begin{equation} \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} = 0 \end{equation} in the first quadrant ## x, y \geq 0 ## with boundary...- Gribouille
- Thread
- Laplace Laplace equation
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

MHB Boundary value problem for Laplace equation
Hello! (Wave) Let $a,b>0$ and $D$ the rectangle $(0,a) \times (0,b)$. We consider the boundary value problem in $D$ for the Laplace equation, with Dirichlet boundary conditions, $\left\{\begin{matrix} u_{xx}+u_{yy}=0 & \text{ in } D,\\ u=h & \text{ in } \partial{D}, \end{matrix}\right.$...- evinda
- Thread
- Boundary Boundary value problem Laplace Laplace equation Value
- Replies: 16
- Forum: Differential Equations
-

How Do You Solve the Laplace Equation in 2D Using Separation of Variables?
Homework Statement Solve the Laplace equation in 2D by the method of separation of variables. The problem is to determine the potential in a long, square, hollow tube, where four walls have different potential. The boundary conditions are as follows: V(x=0, y) = 0 V(x=L, y) = 0 V(x, y=0) = 0...- Selveste
- Thread
- 2d Laplace Laplace equation
- Replies: 1
- Forum: Advanced Physics Homework Help
-
B
Undergrad Can the Schrodinger equation satisfy Laplace's equation?
The time-dependent Schrödinger equation is given by: ##-\frac{\hslash^{2}}{2m}\triangledown^{2}\psi+V\psi=i\hslash\frac{\partial }{\partial t}\psi## Obviously, there is a laplacian in the kinetic energy operator. So, I was wondering if the equation was rearranged as...- bb1414
- Thread
- Laplace equation Laplace's equation Quantum and general physics Schrödinger Schrodinger equation Spherical harmonics
- Replies: 3
- Forum: Quantum Physics
-
H
Graduate Applying boundary conditions on an almost spherical body
I am solving the Laplace equation in 3D: \nabla^{2}V=0 I am considering azumuthal symmetry, so using the usual co-ordinates V=V(r,\theta). Now suppose I have two boundary conditions for [V, which are: V(R(t)+\varepsilon f(t,\theta),\theta)=1,\quad V\rightarrow 0\quad\textrm{as}\quad...- hunt_mat
- Thread
- Body Boundary Boundary conditions Conditions Green's function Laplace equation Spherical
- Replies: 2
- Forum: Differential Equations
-
F
Electric potential outside an insulator in a uniform field
Homework Statement An Ohmic material with some conductivity has a uniform current density J initially. Let's say the current is flowing in the direction of the z-axis. A small insulating sphere with radius R is brought inside the material. Find the potential outside the sphere. Homework...- frimidis
- Thread
- Electric Electric potential Field Insulator Laplace equation Outside Potential Uniform Uniform field
- Replies: 1
- Forum: Advanced Physics Homework Help
-

Point charge with grounded conducting planes angled 120
Homework Statement The problem states: "A point charge q is located at a fixed point P on the internal angle bisector of a 120 degree dihedral angle between two grounded conducting planes. Find the electric potential along the bisector." Homework Equations ΔV = 0 with Dirichlet boundary...- lightest
- Thread
- Charge Conducting Integral equation Laplace equation Planes Point Point charge
- Replies: 3
- Forum: Advanced Physics Homework Help
-
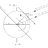
Graduate Laplace Equation for an annular geometry with different BC
Dear all, I would need mathematical help to solve for the temperature field in an annular geometry (you find a picture attached below the text): A copper pipe containing a boiling two-phase flow (in the stratified regime) is immersed in a liquid bath, which temperature ##T_{IY}## is assumed to...- stockzahn
- Thread
- Geometry Laplace Laplace equation
- Replies: 7
- Forum: Differential Equations
-
V
Find potential between 2 conc. cyl. with grounded strip
Homework Statement Two concentric cylinders with radii a & b (b>a) with an infinitely long grounded strip along the z-direction are given potentials \phi_1 and \phi_2. Find \Phi(r,\phi) for a<r<b Boundary conditions: \Phi(r,2n\pi)=0 \Phi(a,\phi)=\phi_1 \Phi(b,\phi)=\phi_2 Homework...- vemarli
- Thread
- Electrostatics Laplace equation Potential
- Replies: 2
- Forum: Advanced Physics Homework Help
-
C
Graduate Laplace equation- variable domain
Hi, I need to solve Laplace equation ## \nabla ^2 \Phi(z,r)=0## in cylindrical coordinates in the domain ## r_1<r<r_2 ##, ## 0<z<L ##. The boundary conditions are: ## \left\{ \begin{aligned} &\Phi(0,r)=V_B \\ &\Phi(L,r)=V_P \\ & -{C^{'}}_{ox} \Phi(x,r_2)=C_0 \frac{\partial \Phi(x,r)}{\partial...- chimay
- Thread
- Domain Laplace Laplace equation Variable
- Replies: 2
- Forum: Differential Equations
-
H
Graduate Problems with identities involving Legendre polynomials
I am studying the linear oscillation of the spherical droplet of water with azimuthal symmetry. I have written the surface of the droplet as F=r-R-f(t,\theta)\equiv 0. I have boiled the problem down to a Laplace equation for the perturbed pressure, p_{1}(t,r,\theta). I have also reasoned that...- hunt_mat
- Thread
- identities Laplace equation Legendre Legendre polynomials Polynomials
- Replies: 16
- Forum: Differential Equations
-
R
Boundary conditions in dielectric problems
Q) A conducting sphere of radius R floats half submerged in a liquid dielectric medium of permittivity e1. The region above the liquid is a gas of permittivity e2. The total free charge on the sphere is Q. Find a radial inverse-square electric field satisfying all boundary conditions and...- RickRazor
- Thread
- Boundary Boundary conditions Conditions Dielectric Dielectric constant Electro statics potential Electrostatic Laplace equation
- Replies: 2
- Forum: Introductory Physics Homework Help
-
C
Undergrad Laplace equation boundary conditions
Hi, I need to solve Laplace equation ##\nabla ^2 \Phi(z,r)=0## in cylindrical coordinates in the domain ##r_1<r<r_2##, ##0<z<L##. The boundary conditions are: ## \left\{ \begin{aligned} &\Phi(0,r)=V_B \\ &\Phi(L,r)=V_P \\ & -{C^{'}}_{ox} \Phi(x,r_2)=C_0 \frac{\partial \Phi(x,r)}{\partial...- chimay
- Thread
- Boundary Boundary conditions Conditions Laplace Laplace equation
- Replies: 6
- Forum: Differential Equations
-

Graduate 2D Cartesian Laplace equation with a single point diffusion
Hi. I have this problem in trying to solve this PDE analytically. The PDE is represented by this diagram: Basically this is solving the Laplace equation with those insulated boundaries except it has that point diffusing its value across the plane. I know how to solve the Laplace equation...- maistral
- Thread
- 2d Cartesian Diffusion Laplace Laplace equation Point
- Replies: 6
- Forum: Differential Equations
-
S
Is Solving Laplace's Equation for a Dielectric Cylinder Straightforward?
Consider an infinitely long hollow dielectric cylinder of radius a with the electricpotential V = V0 cos φ on the surface of the cylinder where φ is an angle measured around the axis of the cylinder. Solve Laplace’s equation to find the electric potential everywhere in space.Do you just plug V...- Sam2000009
- Thread
- Laplace Laplace equation
- Replies: 3
- Forum: Advanced Physics Homework Help