What is Lorentz group: Definition and 69 Discussions

In physics and mathematics, the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical and quantum setting for all (non-gravitational) physical phenomena. The Lorentz group is named for the Dutch physicist Hendrik Lorentz.
For example, the following laws, equations, and theories respect Lorentz symmetry:

The kinematical laws of special relativity
Maxwell's field equations in the theory of electromagnetism
The Dirac equation in the theory of the electron
The Standard Model of particle physicsThe Lorentz group expresses the fundamental symmetry of space and time of all known fundamental laws of nature. In general relativity physics, in cases involving small enough regions of spacetime where gravitational variances are negligible, physical laws are Lorentz invariant in the same manner as that of special relativity physics.

View More On Wikipedia.org
Recent contents Top users
  1. P

    A What's the relationship between RMS framework and the Lorentz group?

    The Robertson-Mansouri-Sexl framework, discussed in "Modern Tests of Lorentz Invariance", https://link.springer.com/article/10.12942/lrr-2005-5?affiliation, is "a well known kinematic test theory for parameterizing deviations from Lorentz invariance." I'm a bit confused on the relationship...
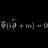
  2. qft-El

    A In what representation do Dirac adjoint spinors lie?

    I hope this is the right section as the question is about Lie groups and representations. First and foremost, in this post I'll be dealing with Dirac and Weyl spinor (not spinor fields) representations of the Lorentz algebra. Also, for simplicity, I'll use the chiral representation later on...
  3. bella987

    Deriving the commutation relations of the Lie algebra of Lorentz group

    This is the defining generator of the Lorentz group which is then divided into subgroups for rotations and boosts And I then want to find the commutation relation [J_m, J_n] (and [J_m, K_n] ). I'm following this derivation, but am having a hard time to understand all the steps: especially...
  4. redtree

    I Why are discontinuous Lorentz transformations excluded from the Poincare group?

    The full Lorentz group includes discontinuous transformations, i.e., time inversion and space inversion, which characterize the non-orthochronous and improper Lorentz groups, respectively. However, these groups are excluded from the Poincare group, in which only the proper, orthochronous...
  5. F

    Deriving Casimir operator from the Lie Algebra of the Lorentz Group

    Hello everyone, I am new here, so please let me know if I am doing something wrong regarding the formatting or the way I am asking for help. I did not really know how to start off, so first I tried to just write out all the ##\mu \nu \rho \sigma## combinations for which ##\epsilon \neq 0## and...
  6. JD_PM

    Discussing the mathematical formalism of generators (Lorentz Group)

    I learned that the Lorentz group is the set of rotations and boosts that satisfy the Lorentz condition ##\Lambda^T g \Lambda = g## I recently learned that a representation is the embedding of the group element(s) in operators (usually being matrices). Examples of Lorentz transformations are...
  7. M

    I Leptons and the Lorentz Group O(3,3)

    This is note about O(3,3) space-time. The related article is: https://doi.org/10.3390/sym12050817 Here's some background: In O(3,1) space-time (Minkowski), the six generators of rotations and boosts can form an SU(2) x SU(2) Lie algebra. This algebra is then used generically by all the...
  8. filip97

    A Product of Representations of Lorentz Group

    How to prove that direct product of two rep of Lorentz group ##(m,n)⊗(a,b)=(m⊗a,n⊗b)## ? Let ##J\in {{J_1,J_2,J_3}}## Then we have : ##[(m,n)⊗(a,b)](J)=(m,n)(J)I_{(a,b)}+I_{(m,n)}⊗(a,b)(J)=## ##=I_m⊗J_n⊗I_a⊗I_b+J_m⊗I_n⊗I_a⊗I_b+I_m⊗I_n⊗J_a⊗I_b+I_m⊗I_n⊗I_a⊗J_b## and...
  9. Jason Bennett

    Lorentz algebra elements in an operator representation

    1) Likely an Einstein summation confusion. Consider Lorentz transformation's defined in the following matter: Please see image [2] below. I aim to consider the product L^0{}_0(\Lambda_1\Lambda_2). Consider the following notation L^\mu{}_\nu(\Lambda_i) = L_i{}^\mu{}_\nu. How then, does...
  10. Jason Bennett

    Lie groups,Lie algebras, Physics, Lorentz Group,

    1) How do we determine a Lie group's global properties when the manifold that it represents is not immediately obvious? Allow me to give the definitions I am working with. A Lie group G is connected iff \forall g_1, g_2 \in G there exists a continuous curve connecting the two, i.e. there...
  11. filip97

    A Why Spinors Are Irreducible if Gamma-Traceless: Explained

    I read this question https://physics.stackexchange.com/questions/95970/under-what-conditions-is-a-vector-spinor-gamma-trace-free . Also I read Sexl and Urbantke book about groups. But I don't understand why spinors is irreducible if these are gamma-tracelees. Also I read many papers about...
  12. filip97

    A (A,A) representation of Lorentz group-why is it tensor?

    Why representation of Lorentz group of shape (A,A) corespond to totally symmetric traceless tensor of rank 2A? For example (5,5)=9+7+5+3+1 (where + is dirrect sum), but 1+5+3+9+7<>(5,5) implies that (5,5) isn't symmetric ? See Weinberg QFT Book Vol.1 page 231.
  13. tomdodd4598

    I Exploring Direct Sums of Lorentz Group Representations

    Hey there, I've suddenly found myself trying to learn about the Lorentz group and its representations, or really the representations of its double-cover. I have now got to the stage where the 'complexified' Lie algebra is being explored, linear combinations of the generators of the rotations...
  14. K

    Vector representation of Lorentz group

    Homework Statement In this problem, we'll construct the ##(\frac{1}{2},\frac{1}{2})## representation which acts on "bi-spinors" ##V_{\alpha\dot{\alpha}}## with ##\alpha=1,2## and ##\dot{\alpha}=1,2##. It is convential, and convenient, to define these bi-spinors so that the first index...
  15. CharlieCW

    General Irreducible Representation of Lorentz Group

    This one may seem a bit long but essentially the problem reduces to some matrix calculations. You may skip the background if you're familiar with Lorentz representations. 1. Homework Statement A Lorentz transformation can be represented by the matrix...
  16. C

    I Lorentz Group: Tensor Representation Explained

    I've been trying to understand representations of the Lorentz group. So as far as I understand, when an object is in an (m,n) representation, then it has two indices (let's say the object is ##\phi^{ij}##), where one index ##i## transforms as ##\exp(i(\theta_k-i\beta_k)A_k)## and the other index...
  17. S

    I What are the best resources for learning about Lorentz group representations?

    Hello! Can someone recommend me some good reading about the Lorentz group and its representations? I want something to go pretty much in all the details (not necessary proofs for all the statements, but most of the properties of the group to be presented). Thank you!
  18. S

    I Understanding 4-Vector Representations in the Lorentz Group

    Hello! I am reading some notes on Lorentz group and at a point it is said that the irreducible representations (IR) of the proper orthochronous Lorentz group are labeled by 2 numbers (as it has rank 2). They describe the 4-vector representation ##D^{(\frac{1}{2},\frac{1}{2})}## and initially I...
  19. M

    I Proof that Galilean & Lorentz Ts form a group

    The Galilean transformations are simple. x'=x-vt y'=y z'=z t'=t. Then why is there so much jargon and complication involved in proving that Galilean transformations satisfy the four group properties (Closure, Associative, Identity, Inverse)? Why talk of 10 generators? Why talk of rotation as...
  20. S

    I Is the Lorentz group non-compact?

    Hello! I need to show that Lorentz Group is non compact, but has 4 connected components. The way I was thinking to do it is to write the relation between the elements of the 4x4 matrices and based on that, associated it with a known topological space, based on the determinant and the value of...
  21. R

    Member of the Poincare or Lorentz Group

    What is more cool... to be a member of the Poincare Group or Lorentz Group? What name would you choose for a school science team and why?
  22. S

    I 6-dimensional representation of Lorentz group

    Hello! I understand that the vector formed of the scalar and vector potential in classical EM behaves like a 4-vector (##A^\nu=\Lambda^\nu_\mu A^\mu##). Does this means that the if we make a vector with the 3 components of B field and 3 of E field, so a 6 components vector V, will it transform...
  23. S

    I Lie Algebra of Lorentz group

    Hello! I read that the for the lie algebra of the Lorentz group we can parametrize the generators as an antisymmetric tensor ##J^{\mu \nu}## and the parameters as an another antisymmetric tensor ##\omega_{\mu \nu}## and a general transformation would be ##\Lambda = exp(-\frac{i}{2} \omega_{\mu...
  24. S

    I Lorentz Group Clarification: Boosts & g Matrix

    Hello! I read that for a boost, for which we have a matrix ##\Lambda## we must satisfy ##\Lambda_\alpha^\mu g_{\mu \nu} \Lambda_\eta^\nu = g_{\alpha \beta}##. I am not sure I understand this. If we have a boost along the x-axis the ##\Lambda_0^0## component is ##\gamma##, but ##\gamma^2 \neq 1 =...
  25. S

    Relativity Lorentz Group Reading: Intro & Math/Phys Perspective

    Hello! Can someone recommend me some good reading about Lorentz and Poincare groups. I would like something that starts from introductory notions but treats the matter both from math (proofs and all that) and physics point of view. Thank you
  26. F

    I Spinor Representation of Lorentz Transformations: Solving the Puzzle

    I've been working my way through Peskin and Schroeder and am currently on the sub-section about how spinors transform under Lorentz transformation. As I understand it, under a Lorentz transformation, a spinor ##\psi## transforms as $$\psi\rightarrow S(\Lambda)\psi$$ where...
  27. T

    I Lorentz group, boost and indices

    Compare this with the definition of the inverse transformation Λ-1: Λ-1Λ = I or (Λ−1)ανΛνβ = δαβ,...(1.33) where I is the 4×4 indentity matrix. The indexes of Λ−1 are superscript for the first and subscript for the second as before, and the matrix product is formed as usual by summing over...
  28. Heisenberg1993

    A Real parameters and imaginary generators

    I was reading some lecture notes on super-symmetry (http://people.sissa.it/~bertmat/lect2.pdf, second page). It is stated that ". In order for all rotation and boost parameters to be real, one must take all the Ji and Ki to be imaginary". I didn't understand the link between the two. What does...
  29. S

    A Transformation of the spinor indices of the Weyl operator under the Lorentz group

    The left-handed Weyl operator is defined by the ##2\times 2## matrix $$p_{\mu}\bar{\sigma}_{\dot{\beta}\alpha}^{\mu} = \begin{pmatrix} p^0 +p^3 & p^1 - i p^2\\ p^1 + ip^2 & p^0 - p^3 \end{pmatrix},$$ where ##\bar{\sigma}^{\mu}=(1,-\vec{\sigma})## are sigma matrices.One can use the sigma...
  30. J

    I Commutator between Casimirs and generators for Lorentz group

    The generators ##\{ L^1, L^2 , L^3 , K^1 , K^2 , K^3 \}## of the Lorentz group satisfy the Lie algebra: \begin{array}{l} [L^i , L^j] = \epsilon^{ij}_{\;\; k} L^k \\ [L^i , K^j] = \epsilon^{ij}_{\;\; k} K^k \\ [K^i , K^j] = \epsilon^{ij}_{\;\; k} L^k \end{array} It has the Casimirs C_1 =...
  31. G

    Adjoint representation of Lorentz group

    Hey, There are some posts about the reps of SO, but I'm confused about some physical understanding of this. We define types of fields depending on how they transform under a Lorentz transformation, i.e. which representation of SO(3,1) they carry. The scalar carries the trivial rep, and lives...
  32. Spinnor

    How do I know if some objects represent the Lorentz Group?

    I'm thinking of an object or objects. How do I show that the objects form a representation of the Lorentz group in 1+1 D spacetime? Thanks for any help!
  33. T

    Lie Algebra of Lorentz Group: Weird Notation?

    In Srednicki's text on quantum field theory, he has a chapter on quantum Lorentz invariance. He presents the commutation relations between the generators of the Lorentz group (equation 2.16) as follows: $$[M^{\mu\nu},M^{\rho\sigma}] =...
  34. TrickyDicky

    Electromagnetic tensor and restricted Lorentz group

    How exactly is the EM field tensor related to the proper orthochronous Lorentz group?
  35. V

    Understanding Lorentz Group Generators: Derivation & Step in Eq 15

    Hi, I am trying to understand the derivation of the Lorentz generators but I am stuck. I am reading this paper at the moment: http://arxiv.org/pdf/1103.0156.pdf I don't understand the following step in equation 15 on page 3: \omega^{\alpha}_{\beta}=g^{\alpha\mu}\omega_{\mu\beta} I don't...
  36. maverick280857

    Why is Lorentz Group in 3D SL(2, R)?

    Hi, While reading "Superspace: One Thousand and One Lessons in Supersymmetry" by Gates et al. I came across the following paragraph: Maybe I haven't understood what exactly they're trying to say here, but 1. Why is the Lorentz Group SL(2, R) instead of SL(2, C)? 2. Why is the two-component...
  37. Xenosum

    Lorentz Group = SU(2) x SU(2)?

    In Ryder's Quantum Field Theory it is shown that the Lie Algebra associated with the Lorentz group may be written as \begin{eqnarray} \begin{aligned}\left[ A_x , A_y \right] = iA_z \text{ and cyclic perms,} \\ \left[ B_x , B_y \right] = iB_z \text{ and cyclic perms,} \\ \left[ A_i ,B_j...
  38. L

    Orthochronous subspace of Lorentz group.

    In a Lorentz group we say there is a proper orthochronous subspace. How can I prove that the product of two orthchronous Lorentz matrices is orthochronous? Thanks. Would appreciate clear proofs.
  39. K

    Question on the 2-dim representation of the Lorentz group

    Hello! I'm currently reading some QFT and have passed the concept of Weyl spinors 2-4 times but this time it didn't make that much sense.. We can identify the Lorentz algebra as two su(2)'s. Hence from QM I'm convinced that the representation of the Lorentz algebra can be of dimension (2s_1 +...
  40. K

    The representation of Lorentz group

    The lorentz group SO(3,1) is isomorphic to SU(2)*SU(2). Then we can use two numbers (m,n) to indicate the representation corresponding to the two SU(2) groups. I understand (0,0) is lorentz scalar, (1/2,0) or (0,1/2) is weyl spinor. What about (1/2, 1/2)? I don't get why it corresponds to...
  41. K

    Regarding representations of the Lorentz group

    Hello! I'm currently reading Peskin and Schroeder and am curious about a qoute on page 38, which concerns representations of the Lorentz group. ”It can be shown that the most general nonlinear transformation laws can be built from these linear transformations, so there is no advantage in...
  42. P

    How Do Lorentz Transformations Relate Time-like Four-Momenta in SO^{+}(1,3)?

    I want to determine the orbits of the proper orthochronous Lorentz group SO^{+}(1,3) . If I start with a time-like four-momentum p = (m, 0, 0, 0) with positive time-component p^{0} = m > 0 , the orbit of SO^{+}(1,3) in p is given by: \mathcal{O}(p) \equiv \lbrace \Lambda p...
  43. K

    About the Lie algebra of our Lorentz group

    Hello! I'm currently reading Ryder - Quantum Field Theory and am a bit confused about his discussion on the correpsondence between Lorentz transformations and SL(2,C) transformations on 2-spinor. He writes that the Lie algebra of Lorentz transformations can be satisfied by setting \vec{K}...
  44. T

    Prove that the proper orthochronous Lorentz group is a linear group

    Homework Statement Prove that the proper orthochronous Lorentz group is a linear group. That is SOo(3, 1) = {a \in SO(3, 1) | (ae4, e4) < 0 } where (x,y) = x^T\etay for \eta = [1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 -1] (sorry couldn't work out how to properly display a matrix). Homework...
  45. S

    Representation of Lorentz group and spinors (in Peskin page 38)

    I am very confused by the treatment of Peskin on representations of Lorentz group and spinors. I am confronted with this stuff for the first time by the way. For now I just want to start by asking: If, as usual Lorentz transformations rotate and boost frames of reference in Minkowski...
  46. F

    SU(2) a double cover for Lorentz group?

    SU(2) a double cover for Lorentz group? I'm presently reading the new book, "Symmetry and the Standard Model", by Matthew Robinson. On page 120, he writes, "the Lorentz group (SO(1,3), pg 117) is actually made up of two copies of SU(2). We want to reiterate that this is only true in 1+3...
  47. V

    Irreducible representations of the Lorentz group

    I'm having some difficulty understanding the representation theory of the Lorentz group. While it's a fundamentally mathematical question, mathematicians and physicists use very different language for representation theory. I think a particle physicist will be more likely than a mathematician to...
  48. TrickyDicky

    Lorentz group and the restricted Lorentz group

    It is a well known fact that the Lorentz group of transfornations are linear. Now reading the wiki entry on the LG it spends a good deal explaining its identity component subgroup, the restricted LG group, and it turns out it is isomorphic to the linear fractional transformation group, which are...
  49. C

    Representations of the Lorentz group

    Can anyone recommend some litterature on representations of the Lorentz group. I'm reading about the dirac equation and there the spinor representation is used, but I would very much like to get a deeper understanding on what is going on.
  50. D

    Understanding the Lorentz Group: What does O(1,3) mean?

    I am totally confused about the Lorentz Group at the moment. According to wikipedia, the Lorentz group can be defined as the General Orthogonal Lie Group##O(1,3)##. However, the definition of the GO Lie Group that I know only works when there is a single number inside the bracket, not 2, e.g...
Back
Top