You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
What is Spinors: Definition and 129 Discussions
In geometry and physics, spinors are elements of a complex vector space that can be associated with Euclidean space. Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation. However, when a sequence of such small rotations is composed (integrated) to form an overall final rotation, the resulting spinor transformation depends on which sequence of small rotations was used. Unlike vectors and tensors, a spinor transforms to its negative when the space is continuously rotated through a complete turn from 0° to 360° (see picture). This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms).
It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which case the Lorentz transformations of special relativity play the role of rotations. Spinors were introduced in geometry by Élie Cartan in 1913. In the 1920s physicists discovered that spinors are essential to describe the intrinsic angular momentum, or "spin", of the electron and other subatomic particles.Spinors are characterized by the specific way in which they behave under rotations. They change in different ways depending not just on the overall final rotation, but the details of how that rotation was achieved (by a continuous path in the rotation group). There are two topologically distinguishable classes (homotopy classes) of paths through rotations that result in the same overall rotation, as illustrated by the belt trick puzzle. These two inequivalent classes yield spinor transformations of opposite sign. The spin group is the group of all rotations keeping track of the class. It doubly covers the rotation group, since each rotation can be obtained in two inequivalent ways as the endpoint of a path. The space of spinors by definition is equipped with a (complex) linear representation of the spin group, meaning that elements of the spin group act as linear transformations on the space of spinors, in a way that genuinely depends on the homotopy class. In mathematical terms, spinors are described by a double-valued projective representation of the rotation group SO(3).
Although spinors can be defined purely as elements of a representation space of the spin group (or its Lie algebra of infinitesimal rotations), they are typically defined as elements of a vector space that carries a linear representation of the Clifford algebra. The Clifford algebra is an associative algebra that can be constructed from Euclidean space and its inner product in a basis-independent way. Both the spin group and its Lie algebra are embedded inside the Clifford algebra in a natural way, and in applications the Clifford algebra is often the easiest to work with. A Clifford space operates on a spinor space, and the elements of a spinor space are spinors. After choosing an orthonormal basis of Euclidean space, a representation of the Clifford algebra is generated by gamma matrices, matrices that satisfy a set of canonical anti-commutation relations. The spinors are the column vectors on which these matrices act. In three Euclidean dimensions, for instance, the Pauli spin matrices are a set of gamma matrices, and the two-component complex column vectors on which these matrices act are spinors. However, the particular matrix representation of the Clifford algebra, hence what precisely constitutes a "column vector" (or spinor), involves the choice of basis and gamma matrices in an essential way. As a representation of the spin group, this realization of spinors as (complex) column vectors will either be irreducible if the dimension is odd, or it will decompose into a pair of so-called "half-spin" or Weyl representations if the dimension is even.
View More On Wikipedia.org
It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which case the Lorentz transformations of special relativity play the role of rotations. Spinors were introduced in geometry by Élie Cartan in 1913. In the 1920s physicists discovered that spinors are essential to describe the intrinsic angular momentum, or "spin", of the electron and other subatomic particles.Spinors are characterized by the specific way in which they behave under rotations. They change in different ways depending not just on the overall final rotation, but the details of how that rotation was achieved (by a continuous path in the rotation group). There are two topologically distinguishable classes (homotopy classes) of paths through rotations that result in the same overall rotation, as illustrated by the belt trick puzzle. These two inequivalent classes yield spinor transformations of opposite sign. The spin group is the group of all rotations keeping track of the class. It doubly covers the rotation group, since each rotation can be obtained in two inequivalent ways as the endpoint of a path. The space of spinors by definition is equipped with a (complex) linear representation of the spin group, meaning that elements of the spin group act as linear transformations on the space of spinors, in a way that genuinely depends on the homotopy class. In mathematical terms, spinors are described by a double-valued projective representation of the rotation group SO(3).
Although spinors can be defined purely as elements of a representation space of the spin group (or its Lie algebra of infinitesimal rotations), they are typically defined as elements of a vector space that carries a linear representation of the Clifford algebra. The Clifford algebra is an associative algebra that can be constructed from Euclidean space and its inner product in a basis-independent way. Both the spin group and its Lie algebra are embedded inside the Clifford algebra in a natural way, and in applications the Clifford algebra is often the easiest to work with. A Clifford space operates on a spinor space, and the elements of a spinor space are spinors. After choosing an orthonormal basis of Euclidean space, a representation of the Clifford algebra is generated by gamma matrices, matrices that satisfy a set of canonical anti-commutation relations. The spinors are the column vectors on which these matrices act. In three Euclidean dimensions, for instance, the Pauli spin matrices are a set of gamma matrices, and the two-component complex column vectors on which these matrices act are spinors. However, the particular matrix representation of the Clifford algebra, hence what precisely constitutes a "column vector" (or spinor), involves the choice of basis and gamma matrices in an essential way. As a representation of the spin group, this realization of spinors as (complex) column vectors will either be irreducible if the dimension is odd, or it will decompose into a pair of so-called "half-spin" or Weyl representations if the dimension is even.
View More On Wikipedia.org
-
S
Quantum Clifford Algebra for Quantum Field Theory, Supersymmetry, Supergravity
I'm currently trying to learn Clifford algebra or more specifically spinors, in higher dimensions. My goal is to study AdS/CFT, but an essential part of learning it is to understand SUSY which then needs some element of Clifford algebra in higher dimensions. I have consulted, Introduction to...- shinobi20
- Thread
- Replies: 3
- Forum: Science and Math Textbooks
-
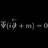
A In what representation do Dirac adjoint spinors lie?
I hope this is the right section as the question is about Lie groups and representations. First and foremost, in this post I'll be dealing with Dirac and Weyl spinor (not spinor fields) representations of the Lorentz algebra. Also, for simplicity, I'll use the chiral representation later on...- qft-El
- Thread
- Replies: 1
- Forum: Differential Geometry
-

I Please help with derivation for Dirac spinors
Could anyone help with some of the later parts of the derivation for Dirac spinors, please? I understand that an arbitrary vector ##\vec v## $$ \begin{bmatrix} x \\ y \\ z \end{bmatrix} $$ can be defined as an equivalent matrix V with the components $$ \begin{bmatrix} z & x - iy \\ x + iy...- James1238765
- Thread
- Replies: 12
- Forum: Quantum Physics
-
H
I Spinors and eigenspinors confusion
Hi, While studying the spin 1/2, I'm facing some confusions about the spinors and the eigenspinors. I understand that ##\chi = \begin{bmatrix}a \\ b \end{bmatrix}## is the spinor with ##\chi_+ = \begin{bmatrix}1 \\ 0 \end{bmatrix}## and ##\chi_-= \begin{bmatrix}0 \\ 1 \end{bmatrix}## the...- happyparticle
- Thread
- Replies: 3
- Forum: Quantum Physics
-
R
I Interpreting ##A^{\mu}(x)|0\rangle## and ##\psi (x) |0\rangle##
I can understand how ##\phi (x)|0\rangle## represents the wavefunction of a single boson localised near ##x##.I don't understand how the same logic appies to ##A^{\mu}(x)|0\rangle## and ##\psi |0\rangle##. Both of these operators return a four component wavefunction when operated on the vaccuum...- Ryder Rude
- Thread
- Replies: 5
- Forum: Quantum Physics
-
G
I Exploring the Relationship Between Spinors and Clifford Algebras
I've used a particular clifford algebra expression for a quantum mechanics wave vector to see if the Born rule can become a simple linear inner product in a clifford algebra formulation. The expression $$\Psi=\sum_i (e_i+Jf_i)\psi_i$$ turned out to be successful, where ##J## is the imaginary...- Gerenuk
- Thread
-
- Tags
- Representation Spinors
- Replies: 2
- Forum: Quantum Physics
-

I How should we interpret the Möbius-strip image of spinors?
On first coming across the Möbius-strip image of spinors, it seemed natural to interpret it as referring to the 3D space of everyday experience, especially as e.g. the Dirac belt and the Penrose book demonstrations appear to occur ‘naturally’ in the world of our phenomenal experience. Doubts...- pellis
- Thread
- Replies: 1
- Forum: Quantum Physics
-

I A Question on Spinors in a High school textbook
While revising Rotational motion, I came across a qualitative question which blew me away. Meaning I couldn't even understand the question let alone answer it😅. It has to do with these objects called spinors which as I understand are evoked in quantum mechanics and Relativity. I am attaching the...- Falgun
- Thread
- Replies: 3
- Forum: Classical Physics
-

Weyl Spinors Transformation, QFT1, Peskin, Chapter 3
\begin{align} \psi_L \rightarrow (1-i \vec{\theta} . \frac{{\vec\sigma}}{2} - \vec\beta . \frac{\vec\sigma}{2}) \psi_L \\ \psi_R \rightarrow (1-i \vec{\theta} . \frac{{\vec\sigma}}{2} + \vec\beta . \frac{\vec\sigma}{2}) \psi_R \end{align} I really cannot evaluate these from boost and rotation...- Pouramat
- Thread
- Replies: 12
- Forum: Advanced Physics Homework Help
-
S
I Matrix construction for spinors
I'm reading the book QFT by Ryder, in the section where ##\rm{SU(2)}## is discussed. First, he considered the group of ##2 \times 2## unitary matrices ##U## with unit determinant such that it has the form, $$U =\begin{bmatrix} a & b \\ -b^* & a^* \end{bmatrix}, \qquad \xi = \begin{bmatrix}...- shinobi20
- Thread
- Replies: 1
- Forum: Quantum Physics
-
S
A Why does equation 35.21 have an extra minus sign?
Eq35.17 and 35.18 is obtained,but the result of Eq35.21 I obtained has an extra minus sign,I don't know what's wrong of my calculation,so I hope some people much more smarter can figure it out.Thanks.- sunshine9
- Thread
- Replies: 1
- Forum: Quantum Physics
-
Q
A Why does the Kähler Potential only contain left handed Weyl spinors?
Why aren't the right handed Weyl spinors included?- QFT1995
- Thread
- Replies: 1
- Forum: Beyond the Standard Models
-

A Vector and Axial vector currents in QFT
I'm currently working out quantities that include the vector and axialvector currents ##j^\mu_B(x)=\bar{\psi}(x)\Gamma^\mu_{B,0}\psi(x)## where B stands for V (vector) or A (axialvector). The gamma in the middle is a product of gamma matrices and the psi's are dirac spinors. Therefore on the...- RicardoMP
- Thread
- Replies: 1
- Forum: Quantum Physics
-

A How to deal with colour indices on spinors
I want to calculate transition amplitudes in QCD for processes like ##q(k)q^\prime(p)\rightarrow q(k^\prime)q^\prime(p^\prime)##, where ##q,q^\prime## are quarks. However, I am unsure what to do with the colour indices of the quark spinors upon squaring the matrix element. For the sake of...- weningth
- Thread
- Replies: 1
- Forum: High Energy, Nuclear, Particle Physics
-

I How Peskin & Schroeder simplified this horrible product of bilinears?
P&S had calculated this expression almost explicitly, except that I didn't find a way to exchange the $$\nu \lambda$$ indices, but I'm sure the below identity is used, $$ \begin{aligned}\left(\overline{u}_{1 L} \overline{\sigma}^{\mu} \sigma^{\nu} \overline{\sigma}^{\lambda} u_{2...- hamad12a
- Thread
- Replies: 5
- Forum: Quantum Physics
-
K
I Time ordering for Dirac spinors
Hello! The time ordered product for Dirac spinors is defined as: $$<0|\psi(x)\bar{\psi}(y)|0>-<0|\bar{\psi}(y)\psi(x)|0>$$ Can someone explain to me how should I think of the dimensionality of this. For a Dirac spinor, ##\psi(x)## is a 4 dimensional column vector, so the first term in that...- kelly0303
- Thread
- Replies: 3
- Forum: High Energy, Nuclear, Particle Physics
-
M
Poincare algebra and its eigenvalues for spinors
Homework Statement Show that for $$W^\mu = -\frac{1}{2}\varepsilon_{\mu\nu\rho\sigma}M^{\nu\rho}P^{\sigma},$$ where ##M^{\mu\nu}## satisfies the commutation relations of the Lorentz group and ##\Psi## is a bispinor that transforms according to the ##(\frac{1}{2},0)\oplus(0,\frac{1}{2})##...- Markus Kahn
- Thread
- Replies: 3
- Forum: Advanced Physics Homework Help
-

MHB Graded Algebra: Understanding Color Dirac Spinors in Space-Time
I just read through a paper on a \mathbb{Z} _ 3 graded Algebra. In this instance we are talking about color Dirac spinors in space-time. It looks like the author is talking about \left ( SU(3) \otimes L^4 \otimes \mathbb{Z}_2 \otimes \mathbb{Z} _2 \right ) \otimes \mathbb{Z} _3. ( SU(3) is...- topsquark
- Thread
-
- Tags
- Algebra Color Dirac Space-time Spinors
- Replies: 2
- Forum: Linear and Abstract Algebra
-

QED Lagrangian in terms of left- and right-handed spinors
Homework Statement I'm stuck at my particle physics exercise about 4-component chiral fields. The following problem is given: "Derive the expression for the QED Lagrangian in terms of the four component right-handed and left-handed Dirac fields ##\Psi_R(x)## and ##\Psi_L(x)##, respectively."...- sebomba
- Thread
-
- Tags
- Lagrangian Qed Spinors Terms
- Replies: 1
- Forum: Advanced Physics Homework Help
-
K
I Weyl Spinors & Helicity: Explained
Hello! So Weyl spinors are 2 dimensional spinors which describe massless particles and have definite helicities. So if we have a right handed Weyl spinor going along the positive x-axis, it's spin will always point along the positive x-axis too. I am a bit confused how can an object have 2 spin...- kelly0303
- Thread
- Replies: 4
- Forum: High Energy, Nuclear, Particle Physics
-
S
I Why are spinors not observables?
Hello! I am reading some QFT and it is a part about how causality implies spin-statistic theorem. In general, one needs 2 observables to commute outside the light-cone. For scalars, we have $$[\phi(x),\phi(y)]=0$$ outside the light-cone, and by using the operator form of the field you get that...- Silviu
- Thread
-
- Tags
- observables Spinors
- Replies: 3
- Forum: Quantum Physics
-
G
Problem Proving a Spinor Identity
Homework Statement Given the spinors: \Psi_{1}=\frac{1}{\sqrt{2}}\left(\psi-\psi^{c}\right) \Psi_{2}=\frac{1}{\sqrt{2}}\left(\psi+\psi^{c}\right) Where c denotes charge conjugation, show that for a vector boson #A_{\mu}#; A_{\mu}\overline{\Psi_{1}}\gamma^{\mu}\Psi_{2} +...- Geremy Holly
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
C
Expectation values and probabilities for spinors in a well
Working on a homework at the moment involving spinors. The algebra isn't hard at all, I just want to make sure my understanding is right and I'm not doing this incorrectly. 1. Homework Statement An electron in a one-dimensional infinite well in the region 0≤x≤a is described by the spinor ψ(x)...- Cameron Roberts
- Thread
- Replies: 2
- Forum: Advanced Physics Homework Help
-

A Transformation of Dirac spinors
So I am working through Lessons in Particle Physics by Luis Anchordoqui and Francis Halzen, the link is https://arxiv.org/PS_cache/arxiv/pdf/0906/0906.1271v2.pdf I am in the discussion of the Dirac equation, on page 21, trying to go from equation 1.5.49 to 1.5.51. And I get stuck. Equation...- Gene Naden
- Thread
- Replies: 3
- Forum: High Energy, Nuclear, Particle Physics
-
S
I Exploring Spinors: A Mathematical and Physical Perspective
Hello! Can someone recommend me some good readings about spinors in physics? I know some basics (i.e. how they work in Minkowski space for Dirac field), but I would like to understand more of the mathematical formalism behind them (how can you build them, in a general number of dimensions, how...- Silviu
- Thread
- Replies: 1
- Forum: High Energy, Nuclear, Particle Physics
-
U
Functional Derivative with respect to Dirac Spinors
Homework Statement I am currently working on an exercise list where I need to calculate the second functional derivative with respect to Grassmann valued fields. $$ \dfrac{\overrightarrow{\delta}}{\delta \psi_{\alpha} (-p)} \left( \int_{x} \widetilde{\bar{\psi}}_{\mu} (x) i \partial_{s}^{\mu...- ur22
- Thread
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
J
A Probability density of dirac spinors
The probability density of the dirac spinor is known to be ∑(Ψ)2 and I know how it is derived. However, I'm just wondering why it should be positive definite. Since the lower two components represent antiparticles, so shouldn't the probability density contribution of those two components be...- Josh1079
- Thread
- Replies: 10
- Forum: High Energy, Nuclear, Particle Physics
-
R
I Pauli spin matrices and Eigen spinors
So I have been studying the case of spin 1/2 and I have understood how the formulations work through to find the spin matrices. However I do not get an intuitive understanding of what they mean and why they are formulated the way they are. I follow Griffith's book and in it as he begins to solve... -
T
Dirac spinors in non-relativistic limit
So, I have to show that in the non-relativistic limit the lower two components of the positive energy solutions to the Dirac equation are smaller than the upper two components by a factor of ##\beta##. I started with the spinor $$\psi = \begin{pmatrix} \phi \\ \frac {\vec \sigma \cdot \vec p}...- Thomas Brady
- Thread
- Replies: 2
- Forum: Advanced Physics Homework Help
-
F
I Spinor Representation of Lorentz Transformations: Solving the Puzzle
I've been working my way through Peskin and Schroeder and am currently on the sub-section about how spinors transform under Lorentz transformation. As I understand it, under a Lorentz transformation, a spinor ##\psi## transforms as $$\psi\rightarrow S(\Lambda)\psi$$ where...- Frank Castle
- Thread
- Replies: 6
- Forum: Special and General Relativity
-

I Understanding the Role of Spinors in Quantum Mechanics
Hey guys, Hope all is well. I'm trying to get my head round some of the Quantum Mechanics of spin. I fully understand why the Pauli equation acts on a two component spinor wavefunction, where I'm a little confused is why the Dirac equation then acts on a 4 component spinor...- Milsomonk
- Thread
- Replies: 2
- Forum: Quantum Physics
-

A Nambu Spinor Notation in Kitaev spinless p-wave model
Hey all! Thanks for reading. I'm currently following along in some reading and had some trouble with re-writing a Hamiltonian in Bogluibov-de Gennes form using Nambu notation (Nambu spinors). Here is the low down: Say we have a Hamiltonian: \frac{1}{2} \sum_{i=1}^{N} c_{i}^{\dagger} D c_{i} +...- DeathbyGreen
- Thread
- Replies: 3
- Forum: Atomic and Condensed Matter
-

I From Pauli spinors to Dirac spinors
Hey guys, Hope all is well. I am trying to understand the process that takes us from the Pauli equation to the Dirac equation. Whilst I understand the motivation is to have a lorrentz covariant equation I don't really understand A.) how this was done B.) what the physical result...- Milsomonk
- Thread
- Replies: 8
- Forum: Quantum Physics
-
V
A How parity exchanges right handed and left handed spinors
Reading through David Tong lecture notes on QFT.On pages 94, he shows the action of parity on spinors. See below link: [1]: http://www.damtp.cam.ac.uk/user/tong/qft/qft.pdfIn (4.75) he confirms that parity exchanges right handed and left handed spinors. Or for an arbitrary representation of...- victorvmotti
- Thread
- Replies: 1
- Forum: Quantum Physics
-
B
A Spinor Lorentz Transform via Vectors - Cross Product Issue
The Lorentz transformation operator acting on an undotted, i.e. right-handed, spinor can be expressed as $$e^{-\frac{1}{2} \sigma \cdot \mathbf{\phi} + i\frac{1}{2} \sigma \cdot \mathbf{\theta}}.$$ There is a very cool, almost childlike, derivation of this expression in Landau Vol. 4 S. 18 I've...- bolbteppa
- Thread
- Replies: 6
- Forum: Quantum Physics
-
S
A Spinors in dimensions other than 4
The Dirac equation describes the behaviour of non-interacting spin-##1/2## fermions in a quantum-field-theoretic framework and is given by ##i\gamma^{\mu}\partial_{\mu}\psi=-m\psi,## where ##\gamma^{\mu}## are the so-called gamma matrices which obey the Clifford algebra...- spaghetti3451
- Thread
-
- Tags
- Dimensions Spinors
- Replies: 3
- Forum: Quantum Physics
-

I Why do Dirac spinors obey the Klein-Gordon equation?
The solutions to the Dirac equation are also solutions of the Klein-Gordon equation, which is the equation of motion for the real scalar field. I can see that the converse is not true, but why do spinors follow the equation for real-field particles? Is there any physical meaning to it?- carllacan
- Thread
-
- Tags
- Dirac Klein-gordon Spinors
- Replies: 8
- Forum: Quantum Physics
-
D
I What kind of space is the space of spinors?
Hi, i don't find much about spinor spaces. I can think in that spaces like a vector space above the field of complex numbers (a complex vector space)? sorry if what i saying is a non-sense, but i really want to understand better the math behind the concept of a spinor. thanks- davi2686
- Thread
- Replies: 4
- Forum: Linear and Abstract Algebra
-
F
A Invariance of Wess Zumino Action under SUSY
Hi guys, I have a very basic question about the WZ model. I want to show that it is invariant under SUSY transformations. The action is \int{d^4 x} \partial^\mu \phi* \partial_\mu \phi +i\psi^† \bar{\sigma}^\mu \partial_\mu \psi The SUSY transformations are \delta\phi = \epsilon \psi ...- fa2209
- Thread
- Replies: 2
- Forum: Beyond the Standard Models
-
F
A Symplectic Majorana Spinors in 5 Dimension
I need to know if the Symplectic Majorana spinors in 5 dimension have any advantage with respect to the Dirac spinors in 5 dimension, since they have the same number of components. For example if the Symplectic Majorana spinors have a manifested symmetry that the Dirac spinors don't have, or if...- Francisca Ramirez
- Thread
- Replies: 5
- Forum: Beyond the Standard Models
-
H
Gordon identity manipulation?
The Gordon identity allows us to solve using $$2m \bar{u}_{s'}(\textbf{p}')\gamma^{\mu}u_{s}(\textbf{p}) = \bar{u}_{s'}(\textbf{p}')[(p'+p)^{\mu} -2iS^{\mu\nu} (p'-p)_{\nu}]u_{s}(\textbf{p}) $$ But how would we solve for $$2m \bar{u}_{s'}(\textbf{p}')\gamma^{\mu}v_{s}(\textbf{p}) $$ Would a...- Higgsy
- Thread
- Replies: 1
- Forum: Atomic and Condensed Matter
-

Explicitly Deriving Spinor Representations from Lorentz Group
I'm currently reading a book on relativistic field theory and I'm trying to understand spinors. After the author introduces the four parts of the Lorentz group he talks about spinors and group representations: "...With this concept we see that the 2x2 unimodular matrices A discussed in the...- JonnyMaddox
- Thread
- Replies: 3
- Forum: Special and General Relativity
-

Representation of Dirac Spinors
Hi there, I have a question with its answer, but, still I don't understand it. Can anybody help me in explaining it? Thanks.- omidaut
- Thread
-
- Tags
- Dirac Representation Spinors
- Replies: 2
- Forum: Quantum Physics
-

Momentum-free spinors and the Dirac equation
We can create a Dirac equation with no potential energy and zero momentum and still get spin? Is this correct? How do the Pauli spin matrices apply here? On the surface, the Dirac equation seems fairly straightforward, but when you dig even a little deeper, it's starts to become unwieldy...- DiracPool
- Thread
-
- Tags
- Dirac Dirac equation Spinors
- Replies: 2
- Forum: Quantum Physics
-
R
Proving Spin Coefficient Transformation for Null Rotation with l Fixed
In Newmann-Penrose formalism, a Null rotation with ##l## fixed is $$l^a−>l^a\\ n^a−>n^a+\bar{c}m^a+c\bar{m}^a+c\bar{c}l^a\\ m^a−>m^a+cl^a\\ \bar{m}^a−>\bar{m}^a+\bar{c}l^a$$ Using this transformation, how to prove? $$π−>π+2\bar{c}ϵ+\bar{c}^2κ+D\bar{c}$$ Ref: 2-Spinors by P.O'Donell, p.no, 65- Ravi Panchal
- Thread
- Replies: 1
- Forum: Special and General Relativity
-

Pseudoscalar current of Majorana fields
Consider a Majorana spinor $$ \Phi=\left(\begin{array}{c}\phi\\\phi^\dagger\end{array}\right) $$ and an pseudoscalar current ##\bar\Phi\gamma^5\Phi##. This term is invariant under hermitian conjugation: $$ \bar\Phi\gamma^5\Phi\to\bar\Phi\gamma^5\Phi $$ but if I exploit the two component...- Andrea M.
- Thread
- Replies: 3
- Forum: High Energy, Nuclear, Particle Physics
-
C
Projection operators and Weyl spinors
I am working through some course notes where the aim is to derive the equations of motion satisfied by the left handed and right handed components of the Dirac spinor ##\psi##. From the Dirac lagrangian, we have $$\mathcal L = \bar \psi (i \not \partial P_L - m P_L)\psi_L + \bar \psi (i \not...- CAF123
- Thread
-
- Tags
- Operators Projection Spinors Weyl
- Replies: 6
- Forum: High Energy, Nuclear, Particle Physics
-
P
Lorentz Transformation on Left & Right Chiral Spinors
I will start with a summary of my confusion: I came across seemingly contradictory transformation rules for left and right chiral spinor in 2 books, and am unable to understand what part is Physics and what part is convention. Or is it that one of the two books incorrectly writes the...- Phys_Reason
- Thread
- Replies: 1
- Forum: High Energy, Nuclear, Particle Physics
-

Barut's Electrodynamics Identity Problem
On page 25 of his book "Electrodynamics and classical theory of fields and particles" he presents this identity \sigma_\mu\sigma_\nu-\frac{i}{2}\epsilon_{\mu\nu\beta\alpha}\sigma^\beta\sigma^\alpha=\delta_{\mu\nu} where \sigma^\mu:(\mathbf{I},-\mathbf{\sigma}) and...- facenian
- Thread
- Replies: 17
- Forum: Special and General Relativity
-
H
SU(2) Rotation & Spinors: Connected?
Hi, a fairly quick question. I'm reading Bruce Schumm's book "Deep Down Things" and he says that in SU(2) you have to rotate by 720 degrees to return to your starting point. This is clearly the same definition as a spinor. My question is, then, does rotation in SU(2) automatically imply the...- HowardTheDuck
- Thread
- Replies: 2
- Forum: Quantum Physics