Zeta function Definition and 106 Threads
-

Undergrad Geometry of series terms of the Riemann Zeta Function
This is an Argand diagram showing the first 40,000 terms of the series form of the Riemann Zeta function, for the argument ##\sigma + i t = 1/2 + 62854.13 \thinspace i## The blue lines are the first 100 (or so) terms, and the rest of the terms are in red. The plot shows a kind of approximate...- Swamp Thing
- Thread
- Function Geometry Riemann Riemann zeta function Series Terms Zeta function
- Replies: 3
- Forum: Topology and Analysis
-

Insights Computing the Riemann Zeta Function Using Fourier Series
Continue reading...- stevendaryl
- Thread
- Computing Fourier Fourier series Function Riemann Riemann zeta function Series Zeta function
- Replies: 5
- Forum: Calculus
-

Graduate Does The Use Of The Zeta Function Bypass Renormalization
I am trying to figure out if the use of the Zeta function allows renormalization to be bypassed. I have formed a preliminary view but would like to hear what others think: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.570.4579&rep=rep1&type=pdf Thanks Bill- bhobba
- Thread
- Function Renormalization Zeta function
- Replies: 3
- Forum: Quantum Physics
-

Undergrad Hausdorff dimension of Riemann zeta function assuming RH
In several places, for example https://xxx.lanl.gov/pdf/chao-dyn/9406003v1, it is claimed that the Riemann zeta function is a fractal under the assumption of a positive result for the Riemann Hypothesis, because (1) the Voronin Universality Theorem, and (2) if the RH is true, then the zeta...- nomadreid
- Thread
- Dimension Function Riemann Riemann zeta function Zeta function
- Replies: 11
- Forum: Topology and Analysis
-

Undergrad Does the Integral of Riemman Zeta Function have a meaning?
I have been trying to use numerical methods with this function but now I realize that I if I could suggest a Polynomial in theory, I could get some value for the Integral at least in any interval. In general, does the Integral of the Riemman dseta function has a meaning by itself?- JorgeM
- Thread
- Function Integral Riemman Zeta function
- Replies: 3
- Forum: Topology and Analysis
-

Undergrad No Way to Solve π(x) from Riemann's Zeta Function?
In the last part of https://en.wikipedia.org/wiki/Riemann_zeta_function#Mellin-type_integrals, I read two expressions of Riemann's zeta function ζ(s) in terms of s and of integrals of the prime-counting function π(x) (the second one using Riemann's prime-counting function J(x) from which, the...- nomadreid
- Thread
- Function Number theory Riemann zeta function Zeta function
- Replies: 9
- Forum: General Math
-
H
High School U-238 spacings and Zeta function zeroes?
I read some old unpublished student notes where the student in an undergrad project was looking at general patterns in QM results. Seemed arbitrary to claim anything but the student did show that spacings in EV between transitions in U238 followed the same general form of zero spacings in the...- houlahound
- Thread
- Function Zeta function
- Replies: 6
- Forum: Beyond the Standard Models
-
P
Graduate String theory and zeta function z(-1)
Over the last couple of years there has been allot of traffic on youtube about the sum of all positive integers being equal to -1/12 as is explained in numberphile video. Some argue that their calculations are wrong and the sum really is infinity. In their original video numberphile shows a...- pcm81
- Thread
- Function String String theory Theory Zeta function
- Replies: 7
- Forum: Beyond the Standard Models
-

Undergrad Quantum Mechanics does Riemann Zeta Function
"Physicists are attempting to map the distribution of the prime numbers to the energy levels of a particular quantum system." https://www.quantamagazine.org/20170404-quantum-physicists-attack-the-riemann-hypothesis/- jedishrfu
- Thread
- Function Mechanics Quantum Quantum mechanics Riemann Riemann zeta function Zeta function
- Replies: 1
- Forum: Quantum Physics
-
D
Graduate Paper About the Riemann Zeta Function
What do you think of the following paper about the Riemann Zeta Function? http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.118.130201- David Neves
- Thread
- Function Paper Riemann Riemann zeta function Zeta function
- Replies: 2
- Forum: General Math
-
M
High School Does the Riemann Hypothesis Follow from the Prime Number Theorem?
There are fewer primes for larger n. The n^1/2 just makes the larger n have less impact on the result. So the riemann hypothesis follows from pnt. Does this make any sense to you?- mustang19
- Thread
- Function Zeta function
- Replies: 1
- Forum: General Math
-

Riemann Zeta Function shows non-trival zeros critical-strip symmetry
1. Homework Statement I want to show that the non-trival zeros of the Riemann Zeta function all lie in the critical strip ## 0 < Re(s) < 1## and further to this that they are symmetric about the line ##Re(s)= 1/2 ## where ## \zeta(s) = \sum\limits^{\infty}_{n=1}n^{-s}## With the functional...- binbagsss
- Thread
- Function Riemann Riemann zeta function Symmetry Zeta function
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
M
High School Does this formula accurately represent the behavior of the zeta function?
Consider Z(s)=Sum(1/N^s) For n=1 to infinity. Let s=(xi+1/2). The divisor is then: N^(xi+1/2) This is equivalent to (N^xi)(N^(1/2)) As n increases, the n^1/2 term will more greatly slow the increase of the divisor and accelerate z(s) away from zero. This means that zeroes will occur less...- mustang19
- Thread
- Behavior Function Zeta function
- Replies: 13
- Forum: General Math
-

Riemann Zeta Function showing converges uniformly for s>1
Homework Statement ## g(s) = \sum\limits^{\infty}_{n=1} 1/n^{-s}, ## Show that ##g(s)## converges uniformly for ## Re(s>1) ## Homework Equations Okay, so I think the right thing to look at is the Weistrass M test. This tells me that if I can find a ##M_{n}##, a real number, such that for...- binbagsss
- Thread
- Function Riemann Riemann zeta function Zeta function
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
M
Graduate Has anything similar to the Riemann hypothesis ever solved
Has anything similar to the Riemann hypothesis ever been solved? Specifically, has anyone proven that the real part of a result of some particular function always assumes a particular value?- mustang19
- Thread
- Riemann Riemann hypothesis Zeta function
- Replies: 2
- Forum: General Math
-
A
High School Can Riemann zeta function be written as ##f(s)=u(s)+iv(s)##?
I don't recall that I have seen Riemann zeta function put in the form of ##f(s)=u(s)+iv(s)##.- Adel Makram
- Thread
- Function Riemann Riemann zeta function Zeta function
- Replies: 1
- Forum: Topology and Analysis
-

Undergrad Riemann zeta: regularization and universality
I am not sure which is the appropriate rubric to put this under, so I am putting it in General Math. If anyone wants to move it, that is fine. Two questions, unrelated except both have to do with the Riemann zeta function (and are not about the Riemann Hypothesis). First, in...- nomadreid
- Thread
- Regularization Riemann Zeta function
- Replies: 1
- Forum: General Math
-

MHB Is the series $ \sum_{n=2}^{\infty} \frac{1}{n^2} $ converges?
Hi - just done the integral test on the Riemann zeta series, came out to $\frac{1}{p-1}$ I can clearly see it therefore converges for P > 1, is singular for p=1, but for p < 1 I can't see why it diverges? In the limit p < 1 just gets smaller? Would also like to check about p = 1, all I need... -
L
Graduate Functional equation Riemann Zeta function
There are two forms of Riemann functional equation. One is more symmetric and follows from the other and the duplication theorem of the Gamma function. At least, that's been claimed here... -

Graduate Distribution of the zeros of the zeta function
In http://www.americanscientist.org/issues/pub/the-spectrum-of-riemannium/5, the author mentions that the function P(x) = 1-(sin(πx)/(πx))2 seems to be, assuming the Riemann Hypothesis is true, to the two-point correlations of the zeros of the Riemann zeta function. Going by...- nomadreid
- Thread
- Distribution Function Zeta function
- Replies: 3
- Forum: Set Theory, Logic, Probability, Statistics
-
T
Graduate Simple Riemann zeta function algebra help
Hi It's just that last step I'm not getting, so you have: [1 / Kz] - [1 / (2K)z] = [ (2K)z - Kz ] / [(2K)z * Kz] = [ (2)z - 1 ] / [(2K)z*] Then what? Thanks- tim9000
- Thread
- Algebra Function Riemann Riemann zeta function Zeta function
- Replies: 7
- Forum: General Math
-
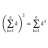
Graduate Why are Ramanujan sums the same as the complex Zeta values?
Possibly a difficult question, but I've never found a discussion on the topic. Thanks- ddd123
- Thread
- Complex Sums Zeta function
- Replies: 3
- Forum: General Math
-
V
Graduate Physical applications of Riemann zeta function
Hi I was wondering if there any observations that have only been described using the Riemann Zeta function? What would it mean in physics to assign a divergent series a finite value? Thank you Edit Sorry I overlooked a thread just posted that asked about this so this might need to be deleted.- vancouver_water
- Thread
- Applications Function Physical Riemann Riemann zeta function Zeta function
- Replies: 9
- Forum: Beyond the Standard Models
-
S
Graduate Generating function for the zeta function of the Hamiltonian
Given a Hamiltonian ##H##, with a spectrum of eigenvalues ##\lambda##, you can define its zeta function as ##\zeta_H(s) = tr \frac{1}{H^s} = \sum_{\lambda}^{} \frac{1}{\lambda^s}##. Subsequently, the log determinant of ##H## with a spectral parameter ##m^2## acts as a generating function for...- spaghetti3451
- Thread
- Function Hamiltonian Zeta function
- Replies: 7
- Forum: Quantum Physics
-
W
Graduate Question about Riemann Zeta Function
I understand how to calculate values of positive values ζ(s), it's pretty straightforward convergence. But when you expand s into the complex plane, like ζ(δ+bi), how do you assign a value with i as an exponent? Take for example ζ(1/2 + i) This is the sequence 1/1^(1/2+i) + 1/2^(1/2+i) +...- willr12
- Thread
- Function Riemann Riemann zeta function Zeta function
- Replies: 2
- Forum: Topology and Analysis
-

Graduate Conjecture about the Prime Zeta Function
I was fooling around with the Prime Zeta Function just recently. Prime Zeta Function, P(s), is defined as Σ1/(p^s), where p is each successive prime. When inputting various positive integer values for (s) on wolfram alpha, I noticed a pattern. Well, an approximate pattern, I should say. My...- David Carroll
- Thread
- Conjecture Function Prime Zeta function
- Replies: 1
- Forum: General Math
-
B
MHB Inequality involving Zeta Function
Prove that for $r>2$ we have $$\frac{\zeta\left(r\right)}{\zeta\left(2r\right)}<\left(1+\frac{1}{2^{r}}\right)\frac{\left(1+3^{r}\right)^{2}}{1+3^{2r}}.$$ I've tried to write Zeta as Euler product but I haven't solve it.- Bibubo
- Thread
- Function Inequality Zeta function
- Replies: 8
- Forum: General Math
-
S
Zeta function regularization and quantum field theory
Homework Statement Hi I need to regularize \sum_{r \in Z+1/2} r In my opinion there are two ways of going about it either re-express it as \sum_{r \in Z+1/2} r = \sum_{r =1} r - \frac{1}{2} \sum_{r =1} = \zeta (-1) - \zeta (0) = \frac{1}{6} or \sum_{r \in Z+1/2} r =...- sgd37
- Thread
- Function Zeta function
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

MHB Derivatives and Integrals of the Hurwitz Zeta function
Initially, the purpose of this tutorial will be to explore and evaluate various lower order derivatives of the Hurwitz Zeta function. In each case, the Hurwitz Zeta function will be differentiated with respect to its first parameter. A little later on - although this will take some time! - these...- DreamWeaver
- Thread
- Derivatives Function Integrals Zeta function
- Replies: 2
- Forum: Math Guides, Tutorials and Articles
-
C
Graduate Can Riemann's Analytic Continuation Solve My Reimann Zeta Function Error?
I am currently writing a c++ program to calculate the Value of the Reimann Zeta Function, The problem is At the state its at, when you input a number a + bi it only gives the correct answer to values of a > 1. Can anyone show or link me Riemann's Analytic continuation of the Function so it... -
N
Graduate Zeta Function -1 1/2 and prime numbers
I talked with an old friend of mine. We discussed prime numbers and Ulams Spiral, and the mathematical patterns that surround us all. He brought up something called the Zeta-Function and something about -1 1/2 and how this all related to prime numbers. I did a google search and found some...- Niaboc67
- Thread
- Function Numbers Prime Prime numbers Zeta function
- Replies: 1
- Forum: General Math
-

MHB Trigonometric series related to the Hurwitz Zeta function
This thread is dedicated to exploring the trigonometric series shown below. This is NOT a tutorial, so all and any contributions would be very much welcome... (Heidy)$$\mathscr{S}_{\infty}(z)= \sum_{k=1}^{\infty}\frac{\log k}{k^2}\cos(2\pi kz)$$ This series can be expressed in terms of the...- DreamWeaver
- Thread
- Function Series Trigonometric Zeta function
- Replies: 11
- Forum: Topology and Analysis
-

MHB The Euler Maclaurin summation formula and the Riemann zeta function
The Euler-Maclaurin summation formula and the Riemann zeta function The Euler-Maclaurin summation formula states that if $f(x)$ has $(2p+1)$ continuous derivatives on the interval $[m,n]$ (where $m$ and $n$ are natural numbers), then $$ \sum_{k=m}^{n-1} f(k) = \int_{m}^{n} f(x) \ dx -... -
D
Inverse of the Riemann Zeta Function
Homework Statement I wish to prove that for s>1 $$ \sum\limits_{n=1}^{\infty}\frac{\mu(n)}{n^s}=\prod_{p}(1-p^{-s})=\frac{1}{\zeta(s)}. $$ The Attempt at a Solution (1) I first showed that $$ \prod_{p}(1-p^{-s})=\frac{1}{\zeta(s)}. $$ It was a given theorem in the text that $$...- DeadOriginal
- Thread
- Function Inverse Riemann Riemann zeta function Zeta function
- Replies: 8
- Forum: Calculus and Beyond Homework Help
-

MHB A curiosity about the Riemann Zeta Function....
Recently some interesting material about the Riemann Zeta Function appeared on MHB and I also contributed in the post... http://mathhelpboards.com/challenge-questions-puzzles-28/simplifying-quotient-7235.html#post33008 ... where has been obtained the expression... $\displaystyle \zeta (s) =...- chisigma
- Thread
- Curiosity Function Riemann Riemann zeta function Zeta function
- Replies: 10
- Forum: Topology and Analysis
-

MHB An integral representation of the Hurwitz zeta function
For $ \text{Re} (a) >0$ and $\text{Re} (s)>1$, the Hurwitz zeta function is defined as $ \displaystyle \zeta(s,a) = \sum_{n=0}^{\infty} \frac{1}{(a+n)^{s}} $. Notice that $\zeta(s) = \zeta(s,1)$. So the Hurwitz zeta function is a generalization of the Riemann zeta function. And just like the... -

MHB Another integral representation of the Riemann zeta function
Here is another integral representation of $\zeta(s)$ that is valid for all complex values of $s$. It's similar to the first one, but a bit harder to derive.$ \displaystyle \zeta(s) = 2 \int_{0}^{\infty} \frac{\sin (s \arctan t)}{(1+t^{2})^{s/2} (e^{2 \pi t} - 1)} \ dt + \frac{1}{2} +... -

MHB An integral representation of the Riemann zeta function
Show that $\displaystyle \zeta(s) = \frac{2^{s-1}}{1-2^{1-s}} \int_{0}^{\infty} \frac{\cos (s \arctan t)}{(1+t^{2})^{s/2} \cosh \left( \frac{\pi t}{2} \right)} \ dt $The cool thing about this representation is that it is valid for all complex values of $s$ excluding $s=1$. This integral is...- polygamma
- Thread
- Function Integral Representation Riemann Riemann zeta function Zeta function
- Replies: 1
- Forum: Topology and Analysis
-

MHB What are the $\rho$ values in the zeros of the Zeta function?
In an article it is given that, $$\zeta(s)=\text{exp} (\sum_{n=1}^\infty\frac{\Lambda{(n)}}{\text{log}(n)}n^{-s})$$ $\zeta(s)$ has pole at $s=1$ and zeroes at several $s=\rho$. here i think he considered the function inside the exponential rather than whole exponential to obtain poles and...- mathworker
- Thread
- Function Zeta function
- Replies: 1
- Forum: Topology and Analysis
-
L
Undergrad I'm trying to write a program that plots the riemann zeta function
I saw a picture of what it might look like when I was researching it, but I'm confused about something. The picture's caption said that the complex coordinates were darkened as their value got larger, leading to a helpful graph, but I do not understand what scale they used. For my program, I...- LastTimelord
- Thread
- Function Plots Program Riemann Riemann zeta function Zeta function
- Replies: 1
- Forum: Linear and Abstract Algebra
-
P
Graduate Zeta function for Debye Low Temp. Limit
Hello, In the low temp. limit of Debye law for specific heat, we encounter the following integral: ∫(x4 ex)/(ex-1)2 dx, from 0 to ∞. The result is 4∏2/15. I have searched and found this to be related to zeta function but zeta functions do not have ex in the numerator so I am unable...- phys_student1
- Thread
- Debye Function Limit Zeta function
- Replies: 1
- Forum: Calculus
-
S
Graduate What Does the Third Axis Represent in Riemann Zeta Function Zeros Graphs?
I was looking at the Wolfram Alpha page on the Riemann Zeta Function Zeros which can be found here, http://mathworld.wolfram.com/RiemannZetaFunctionZeros.html At the top of the pag there are three graphs each with what looks to be a hole through the graph. Now I know the graph is an Argand...- SpaceDreamer
- Thread
- Function Riemann Riemann zeta function Zeta function
- Replies: 1
- Forum: Topology and Analysis
-
C
Graduate About interesting convergence of Riemann Zeta Function
Hi, I was playing with Riemann zeta function on mathematica. I encountered with a quite interesting result. I iterated Riemann zeta function for zero. (e.g Zeta...[Zeta[Zeta[0]]]...] It converges into a specific number which is -0.295905. Also for any negative values of Zeta function, iteration...- cryptist
- Thread
- Convergence Function Interesting Riemann Riemann zeta function Zeta function
- Replies: 10
- Forum: Linear and Abstract Algebra
-

Graduate Riemann's zeta function fractal because of Voronin?
Riemann's zeta function "fractal" because of Voronin? I am not sure which rubric this belongs to, but since the zeta function is involved, I am putting it here. I noticed a comment (but was in too much of a hurry to remember the source) that, because of the "universality" of the Riemann zeta...- nomadreid
- Thread
- Fractal Function Zeta function
- Replies: 2
- Forum: Linear and Abstract Algebra
-
S
Undergrad Is Riemann Zeta function related to differential equations?
Hi. I just came back from my differential equation midterm and was surprised to see a problem with the Riemann-zeta equations on it. I think the problem went something like "Prove that \pi/6 = 1 + (1/2)^2 + (1/3)^2 + ... " The study guide did mention that "prepare for a problem or two...- stgermaine
- Thread
- Differential Differential equations Function Riemann Riemann zeta function Zeta function
- Replies: 4
- Forum: Differential Equations
-

Discovering Prime Numbers & Riemann's Zeta Function
Hi everybody. I would like to find a book about the Distribution of Prime Numbers and the Riemann's Zeta Function. I know about the "classical" books: 1) Titchmarsh's "The Theory of the Riemann Zeta-Function" 2) Ingham's "The Distribution of Prime Numbers" 3) Ivic's "The Riemann...- Karlx
- Thread
- Function Numbers Prime Prime numbers Zeta function
- Replies: 2
- Forum: Science and Math Textbooks
-
M
Graduate Euler's derivation of Riemann Zeta Function for even integers
So Euler derived the analytic expression for the even integers of the Riemann Zeta Function. I was wondering if there is a link to his derivation somewhere? Also, is there anyone else who used a different method to get the same answer as Euler? Thank you- Mugged
- Thread
- Derivation even Function Integers Riemann Riemann zeta function Zeta function
- Replies: 2
- Forum: General Math
-
K
Which book is the best for understanding the Riemann hypotheses?
I'm looking for a semi-popular book on the Riemann hypotheses, on the scale of Derbyshire's book. It seems that Derbyshire and Edwards are the best in this area. Which one should I go for? The content must be quite extensive. Please suggest other ones too...- khil_phys
- Thread
- Books Function Zeta function
- Replies: 1
- Forum: Science and Math Textbooks
-
M
Graduate Zeta function the the orime counting function
i have a question about the relation between the riemann zeta function and the prime counting function . one starts with the formal definition of zeta : \zeta (s)=\prod_{p}\frac{1}{1-p^{-s}} then : ln(\zeta (s))= -\sum_{p}ln(1-p^{-s})=\sum_{p}\sum_{n=1}^{\infty}\frac{p^{-sn}}{n} using the... -
K
Graduate Riemann zeta function - one identity
Let p_n be number of Non-Isomorphic Abelian Groups by order n. For R(s)>1 with \zeta(s)=\sum_{n=1}^{\infty}\frac{1}{n^s} we define Riemann zeta function. Fundamental theorem of arithmetic is biconditional with fact that \zeta(s)=\prod_{p} (1-p^{-s})^{-1} for R(s)>1. Proove that for R(s)>1 is...