2-bit Bin Full Adder Truth Table Derivation

[jisbon]

Homework Statement

-

Relevant Equations

-

Hi all,
I am having some troubles deriving the truth table of the following:
I don't understand how does one gets to the highlight parts. For example, 10 10, when the carry is low, shouldn't the output be 0 0 1?

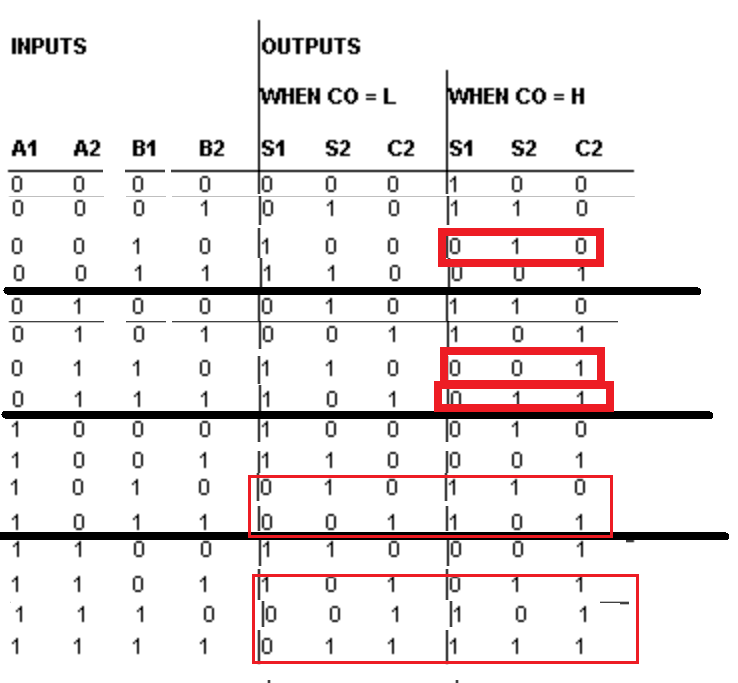
I fully understand how to add if it is a single bit, but now with 2 bits, it is a bit confusing and I can't seem to find any resources online to learn about this :( Any help will be appreciated.

 

[Merlin3189]

Adding two + two bits is just adding one + one bits twice: two single bit full adders.

For a single bit adder, you have three inputs and two outputs.
So the sum is 0, 1, 2, or 3 ie. 00,01,10, or 11.
The LSB out is the bit value and the MSB is the carry.

If you work out the table for the first bit, then for the second bit, you can combine the relevant rows to get the two bit table.

I think the confusing factor in this question isthat they treat the C0 input as in some way different from the A and B inputs. To me, all three inputs to a full adder are equivalent. C0 is just another input along with A1 and B1.

 

[Merlin3189]

Maybe I've jumped the gun! Looking at the example in your comment,

I don't understand how does one gets to the highlight parts. For example, 10 10, when the carry is low, shouldn't the output be 0 0 1?

Looking at your specific example 10 + 10 = 100 it seems your problem may be knowing which bit is which.

In the table it seems to me that bit 1 is LSB and bit 2 is MSB, so
10 + 10 is A1=0, B1=0 , both LSBs; A2=1, B2=1, both MSBs; and the output is LSB S1=0, S2=0 and C2=1 new MSB
That would be the 6th line in the table where C0=0.

 

[jisbon]

Maybe I've jumped the gun! Looking at the example in your comment,

Looking at your specific example 10 + 10 = 100 it seems your problem may be knowing which bit is which.

In the table it seems to me that bit 1 is LSB and bit 2 is MSB, so
10 + 10 is A1=0, B1=0 , both LSBs; A2=1, B2=1, both MSBs; and the output is LSB S1=0, S2=0 and C2=1 new MSB
That would be the 6th line in the table where C0=0.

Oh so I'm reading the table wrongly? 10 +10 is indeed 001?

 

[Merlin3189]

That's my view. It seems a reasonable interpretation and the table makes sense that way.
A and B are the two data streams. A1 and B1 are LSB, A2 and B2 MSB, C0 is the carry in and
for output S1 is bit 0, S2 is bit 1 and C2 is carry out, where bit 0 means LSB.

As I said, I don't like the layout of the table, but I can make sense of it if I understand it in this way.
It is always a problem (IMO) withthese things, that we all have our own way of mapping hardware to semantics. Big endians and little endians caused endless (!) trouble in my day.