hannibalisfun
- 7
- 0
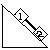
The problem is I have two blocks on an inclined plane. They are connected by a metal rod. The bottom(2) mass provides the dominate force. Fiction is involved. They have different kinetic coefficients of friction. I need to know the acceleration of the system and the tension in the rod. Picture in diagram 1.
If you could provide help on one other problem that would help a lot.
A plane is turning. Yoy know the angle its wings are tilted and its speed. How do you find the radius of the turn? Assume all force come from aerodynamic lift.
If you could provide help on one other problem that would help a lot.
A plane is turning. Yoy know the angle its wings are tilted and its speed. How do you find the radius of the turn? Assume all force come from aerodynamic lift.