omka
Poster warned about not having used the homework template
Hello,
I'm having difficulty finding equation of motion for 3 degree of freedom spring mass system.
Homework Statement
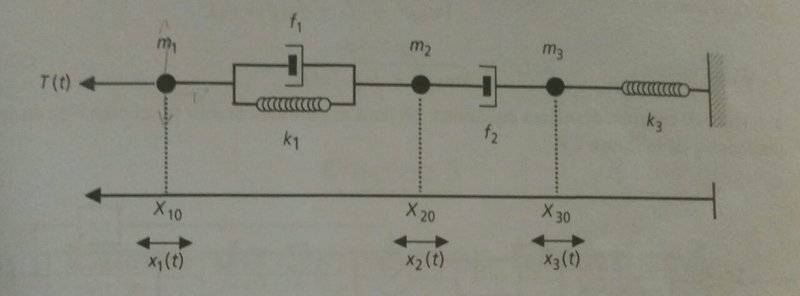
the positions of the masses at the equilibre are respectively X10, X20, X30
At t = 0s, the mass m1 is drawn to the left with the force T (t).
Each of the masses is moved from it's equilibrium position by x1 (t), x2 (t) and x3 (t), respectively.
Write the fundamental equation of the dynamics for m1, m2 and m3
K1 stiffness coefficient spring 1
K3 stiffness coefficient spring 2
f1 f2 f3 viscous coefficient
the fundamental equation of the dynamics
At t= 0s When the mass m1 has moved a distance x1 from it's position (to the left) the spring k1 will be stretched that mean that this spring will be exerting a force on the mass to the right. The viscous force f1 will be exerting also a force on the right because the viscous fiction is always opposite to the direction of motion.
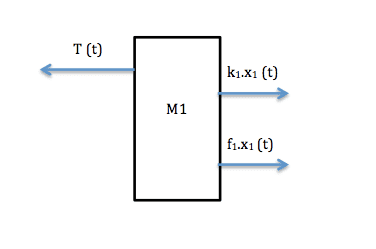
But the motion of m1 depend also of the motion of mass 2 and so of f2.
Could you please help me to understand what are the forces exerted on the mass 1 and mass 2 from the other masses.
I'm having difficulty finding equation of motion for 3 degree of freedom spring mass system.
Homework Statement
the positions of the masses at the equilibre are respectively X10, X20, X30
At t = 0s, the mass m1 is drawn to the left with the force T (t).
Each of the masses is moved from it's equilibrium position by x1 (t), x2 (t) and x3 (t), respectively.
Write the fundamental equation of the dynamics for m1, m2 and m3
K1 stiffness coefficient spring 1
K3 stiffness coefficient spring 2
f1 f2 f3 viscous coefficient
Homework Equations
the fundamental equation of the dynamics
The Attempt at a Solution
At t= 0s When the mass m1 has moved a distance x1 from it's position (to the left) the spring k1 will be stretched that mean that this spring will be exerting a force on the mass to the right. The viscous force f1 will be exerting also a force on the right because the viscous fiction is always opposite to the direction of motion.
But the motion of m1 depend also of the motion of mass 2 and so of f2.
Could you please help me to understand what are the forces exerted on the mass 1 and mass 2 from the other masses.
Attachments
Last edited by a moderator: