Engineering 2 j-terms in a transfer function?

[peasngravy]

Homework Statement

Design and PSPICE model a bandpass filter of ‘Sallen and Key’ topology, having the following characteristics:
fo = 3.3khz
Q=2.2
Verify your design by means of a Bode plot.

Relevant Equations

V2/V1 = -1/ (2R1/R2) + jwCR1 + 1/(jwCR2)

I have the above transfer function for this filter design

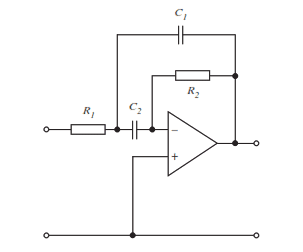
The transfer function becomes

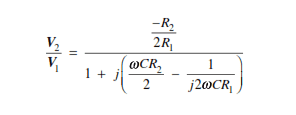
which then becomes

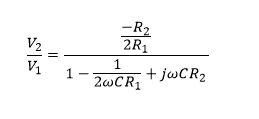
Now when I try to use this transfer function to plot a bode plot, I always end up with negative terms which i can't get the square root of

For example, at 1hz, where
w = 6.283
R1 = 1705
R2 = 33000
C = 6.43nF

I end up with

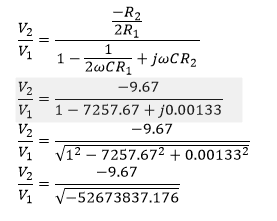
Is anyone able to explain where I am going wrong with this?

Thanks

 

[LvW]

At first, we must clarify the question about the structure (topology) of the filter.
In the text, a "Sallen-Key"-topology is mentioned, but the shown circuit represents another structure (Multi-feedback.) So - what is really your task?

 

[peasngravy]

At first, we must clarify the question about the structure (topology) of the filter.
In the text, a "Sallen-Key"-topology is mentioned, but the shown circuit represents another structure (Multi-feedback.) So - what is really your task?

my task is to design a sallen key band pass filter with an fo value of around 3.3k and a Q factor of 2.2. I believe my main objective is not the design of the circuit itself but to come up with the capacitor and resistor values for those requirements

this topology appears in my course notes under the heading “sallen key bandpass filter”.

 

[LvW]

In this case, your course notes are not correct. The Sallen-Key topology contains a fixed-gain opamp (very often with unity gain, voltage follower) and a second-order RC-network within the feedback path.
Such filters are non-inverting.
Are you required to derive the transfer function by yourself or can you use it as given in relevant books?

Hint: In case of a bandpass, a fixed gain of "2" has some advantages if compared with unity gain (much smaller component spread).

Comment/Correction: When you add in your diagram a resistor R3 in series to C2 , the opamp with the resistors R2 and R3 can be regarded as an INVERTING fixed gain amplifier. In this case, the whole circuit resembles a (less known) "inverting Sallen-Key architecture". So - you now have the choice between 3 alternatives:
* Multi-feedback (your diagram)
* Inverting Sallen-Key (your diagram plus R3)
* Non-inverting (classical) Sallen-Key (new circuit with fixed pos. gain).

 

[gneill]

A Bode plot plots gain in dB versus frequency, either angular (radians/sec) or Hz, your choice. So you don't just plot $V_2/V_1$. Instead you want to plot:
$$U_{dB}(f) = 20 log\left| \frac{V_2}{V_1} \right| $$

Looking at your transfer function and comparing it to the given circuit it seems to me like you've swapped the two resistor values in the denominator terms.

 

[peasngravy]

The circuit I posted does actually also appear in this paper as a sallen-key bandpass filter
http://sites.bu.edu/engcourses/files/2016/08/ActiveFilterNotes.pdf

 

[LvW]

I propose to consult some other knowledge sources - and then you will see that the shown circuit is NOT a "Sallen-Key" type. I suppose, in the book, they have placed a wrong circuit diagram (by accident).

Have a look on Fig. 13.7 and Fig.13-12. Here you see how a Sallen-Key topolgy looks like (unity-gain amplifiers)

 

[peasngravy]

I found this paper on designing them https://www.irjet.net/archives/V2/i5/IRJET-V2I5143.pdf

This may be very helpful to me but I need to fully understand the relationship between s=jw. Imaginary numbers are very new to me and have caused me quite a bit of trouble so far.

 

[peasngravy]

That could very well be my issue - i am glad I know what I did wrong but unfortunately I only know I did wrong on the wrong circuit anyway

 

[LvW]

This paper looks good. And as far as I can see - they have selected a fixed gain of "2" (as I have proposed). So you can use this paper - and the shown design process - as a good reference for solving your task.

 

[peasngravy]

Great - thank you for pointing out that this was incorrect or i'd have used the wrong circuit.

When I have the s term, how do I derive a value for this for a bode plot if it is based on an imaginary term?

 

[peasngravy]

@LvW - I didn't realize you had added further comments to your post above, apologies for not acknowledging them

 

[The Electrician]

Now when I try to use this transfer function to plot a bode plot, I always end up with negative terms which i can't get the square root of

For example, at 1hz, where
w = 6.283
R1 = 1705
R2 = 33000
C = 6.43nF

I end up with

View attachment 274059
Is anyone able to explain where I am going wrong with this?

Thanks

You don't plot the transfer function itself, which is a complex value at each frequency--you plot the magnitude of the transfer function.

If you're going to keep doing this sort of stuff you really should acquire a facility with doing complex arithmetic.

Your transfer function is a fraction with a denominator that has an imaginary part. To evaluate the magnitude of the transfer function you need to get the imaginary parts out of the denominator. This is done by rationalizing the transfer function.

See: http://www.solving-math-problems.com/algebra-rationalize-denominator-with-complex-numbers.html

Then you need to calculate the magnitude of the transfer function at each frequency and plot that magnitude. If you want to plot db you take the base 10 logarithm and multiply by 20. Strictly speaking this would not be a Bode plot, but rather a frequency response plot. See the following links for more about a Bode plot.

See here (also part way through deals with "But wait! We still have j in the equation"): https://blanco.io/education/principles-of-ee-2/how-to-bode-plot/

Additional discussion:

http://faculty.mercer.edu/jenkins_he/documents/bodeplots1.pdf

https://lpsa.swarthmore.edu/Bode/BodeRules.html

 

[The Electrician]

I found this paper on designing them https://www.irjet.net/archives/V2/i5/IRJET-V2I5143.pdf

This may be very helpful to me but I need to fully understand the relationship between s=jw. Imaginary numbers are very new to me and have caused me quite a bit of trouble so far.

Read this: https://en.wikipedia.org/wiki/Sallen–Key_topology

Be sure to check the "External links" at the bottom of that page.

 

[peasngravy]

@The Electrician - thank you for that information.

I got there now, i am quite happy with my result

I also realized I was trying to resolve the magnitude of the complex numbers instead of just using the excel functions available (i don't have any software like MATLAB or mathcad whch would've made this far easier)