2 Masses, Friction, Inclined Plane, Pulley problem

[shaggyster]

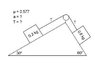
Here's a problem I've been having trouble with. I was hoping someone out there can give me some insight on it. Basically it's just two masses both coupled together with a massless rope on a frictionless and massless pulley on an inclined plane WITH friction. Here's the diagram. The problem is to figure out the tension in the rope and the acceleration of the blocks.

 

[Pyrrhus]

Well, use Newton's 2nd Law, and pick a direction for the acceleration.

\sum_{i=1}^{n} \vec{F}_{i} = m \vec{a}

Also remember

F_{f} = \mu N

 

[pseudonewtonian]

you get two dynamical equations... In which there are only two unknowns... Tension and acceleration... frictional force is known... Two equations two variables...Voila ! Theres your answer