2 Objects connected by rigid rod moving perpendicular to each other

[physacks]

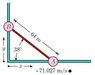
I am having a lot of trouble trying to figure out ot do this problem. The problem states that Two objects, A and B are connected by a rigid rod that has a length of 60m. The objects slide along perpendicular guide rails. If A slides to the left witha constant speed of 62m/s along the x-axis, find the velocity of B along the Y-axis when the rod makes an angle 30 degrees with the X-axis.

I have tried to work out this using trig functions but I do not think that is the proper way of doing the problem. Feel free to change the numbers around, I really just want to understand how to do the problem as I am stuck. I have been unable to figure it out by reading my book and cannot find a similar problem.

Thanks for the help!

 

[Doc Al]

Hint 1: What's the relationship between the two coordinates? (Think Pythagorus.)

Hint 2: You'll need to take a derivative.

 

[jsliv03]

I have a similar problem to the one physacks submitted. I'm having trouble finding the relationship between the coordinates as you (Doc Al) said.
Plz help,
Thanks

 

[Doc Al]

Please provide a diagram that illustrates the problem. I assume that object A is constrained to move along the x-axis and object B is constrained to move along the y-axis. Since the distance between the two end points is fixed, how must the positions of the two objects relate? Hint: The origin and the objects A and B form a right triangle whose hypotenuse is the length of the rod.

 

[jsliv03]

Here's the diagram of the problem.
I assume the sides are related by the pythagorean theorem: x^2 + y^2 = 64^2
Do I take the derivative of this equation or is there another equation I need? I feel like I need something that also relates time. It seems like a rate of change problem...so I'd use an implicit derivative. But I'm just having trouble figuring out the equation to use.
Thanks

 

[Dr.D]

jslive03, try thinking of your equation as
[x(t)]^2+[y(t)]^2=64^2
and then differentiate wrt t.

By the way, this is called a trammel mechanism.

 

[Doc Al]

I assume the sides are related by the pythagorean theorem: x^2 + y^2 = 64^2
Do I take the derivative of this equation or is there another equation I need?

You're doing fine. That's the equation you need.

I feel like I need something that also relates time. It seems like a rate of change problem...so I'd use an implicit derivative.

Exactly.

Now just work out how the 38 degrees fits in.