What happens when two springs are connected in series and then cut?

[musicfairy]

In Figure 7-52, two identical springs, each with a relaxed length of 50 cm and a spring constant of 400 N/m, are connected by a short cord of length 10 cm. The upper spring is attached to the ceiling. A box that weighs 105 N hangs from the lower spring. Two additional cords, each 85 cm long, are also tied to the assembly, and they are limp.

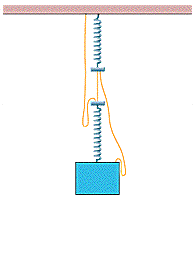
(a) If the short cord is cut, so that the box then hangs from the springs and the two longer cords, does the box move up or down from its initial location?

(b) How far does the box move?

(c) How much total work do the two spring forces (one directly, the other via a cord) do on the box during that move?



The springs are supposed to change from series to || when the cord is cut. I have a very hard time visualizing what it would look like.

For part a it moves up.

For part b I try to solve for the length of the whole thing by adding the length of the spring and cord, then solving for how far it stretches.

F = kx
105 = 400x
x = 0.26 m

Since there's 2 spring the length stretched would be 0.52 m

So I added the distance stretched to thye length of the two springs and the short cord, and got 1.02 m.

Now I have to figure out the new length. The 2 springs are in ||, so they'll stretch half as much. What I don't know is what to do with the 2 springs. I can't visualize, so I can't solve for the change in length.

I can't do part c unless I have unless I get an answer from part b. I assume that the work done would be be the change in distance stretched? I'm not really sure.




Please help.

 

[Q_Goest]

(a) If the short cord is cut, so that the box then hangs from the springs and the two longer cords, does the box move up or down from its initial location?
For part a it moves up.

Not sure if I agree or not, but could you show your work?

For part b I try to solve for the length of the whole thing by adding the length of the spring and cord, then solving for how far it stretches.

F = kx
105 = 400x
x = 0.26 m

Since there's 2 spring the length stretched would be 0.52 m

So I added the distance stretched to thye length of the two springs and the short cord, and got 1.02 m.

Good! You found the original distance the box is hanging. But that doesn't say how far up or down it moves. Consider that the two springs are as you say, in parallel, right? So the sum of the forces should be zero if in equilibrium. You have two springs creating a force up and a weight creating a force down. Equate the two.

(c) How much total work do the two spring forces (one directly, the other via a cord) do on the box during that move?

The springs are supposed to change from series to || when the cord is cut. I have a very hard time visualizing what it would look like.
...
Now I have to figure out the new length. The 2 springs are in ||, so they'll stretch half as much. What I don't know is what to do with the 2 springs. I can't visualize, so I can't solve for the change in length.

I can't do part c unless I have unless I get an answer from part b. I assume that the work done would be be the change in distance stretched? I'm not really sure.

Try visualizing this as two separate springs in parallel with a box hanging below them on strings. Doesn't really matter if the strings are above or below the springs, the calculation doesn't change.

To calculate work done, use the equations for potential energy stored in a spring to find the difference between the original condition and the parallel condition.

Hope that helps.

 

[musicfairy]

The teacher told us that part a is is more visual than math, and that it moves up.

For part b I tried to make the new length the length of the string plus spring and distance stretched, but that woulc make it move down instead of up.

As for c, this is what I did:

For the original, when they're in series:

W = 2(.5)kx²
W = 2(.5)(400)(.26)²
W = 27.04 J

The final:

W = 2(.5)kx²
W = 2(.5)(400)(.13)²
W = 6.76 J

Because each spring is supporting half the weight, the distance stretched is 0.13

So I subtracted the final from the original and got 20.28

Should it be negative because work/force by spring is typically negative?

 

[Q_Goest]

ok, I'm forced to do some math... let's work out how long each spring is with a single bit of the 10 cm cord attached prior to cutting.

Relaxed spring is: .050 m
String is: .010 m
Stretch is: .260 m
Total is .05+.01+.26 = .32 m

cord length (supposed to be loose) is .085 m... hmmm... something doesn't jive wit the picture. Maybe the 85 cm cord is in parallel with the short 10 cm bit and not both spring and short bit... check the original question.

As for c, this is what I did:

For the original, when they're in series:

W = 2(.5)kx²
W = 2(.5)(400)(.26)²
W = 27.04 J

The final:

W = 2(.5)kx²
W = 2(.5)(400)(.13)²
W = 6.76 J

Because each spring is supporting half the weight, the distance stretched is 0.13

So I subtracted the final from the original and got 20.28

Should it be negative because work/force by spring is typically negative?

The way you did the work/spring energy is correct. Generally, work or energy is negative that leaves a system, positive when it enters. So the springs (together) did 20.28 J of work on the box, regardless of whether the box rose or fell since it is the springs doing the work on the box.

You could say, "How much potential energy did the box loose (assuming it fell after sniping the cord) or gain (assuming the box rose after sniping the cord)" and that would be different, since gravity also acts on the box. In that case, you would find the total change in elevation of the box to determine how much energy difference there is. The total energy acting on the box is the sum of the spring plus gravity.

 

[musicfairy]

Apparently 20.28 didn't work for part c. Something's wrong...

So I tried part b using only the length of the springs and length stretched, which turned out to be 63 cm. I subtracted it from the original length and got 39 cm. That didn't work either.

 

[Q_Goest]

The OP said the 85 cm cords are limp. As mentioned previously, this doesn't add up. it has to be taut.

Let's say they are connected in the way indicated by the picture, but in this case, they are actually taut. If they are taut (ie: the springs aren't stiff enough to keep them from going taut) then the amount of stretch on the spring prior to cutting the 10 cm cord is:
85 cm - 10 cm - 50 cm = 25 cm
do you agree?

So the spring energy is what? (ie: stretch x = 25 cm)

Afterwards, springs stretches to x = 130 cm as you have indicated.

calculate work done by springs on box. How does that look?

 

[musicfairy]

Where did you get 85 cm - 10 cm - 50 cm = 25 cm?

 

[Q_Goest]

Where did you get 85 cm - 10 cm - 50 cm = 25 cm?

The unstretched spring is 50 cm.
The short string is 10 cm.
The long string in parallel with these two is 85 cm.
So the most the spring can stretch before it gets taut is 85-50-10=25. Assume the spring can't stretch any further since it is being restrained by the 85 cm string.

 

[musicfairy]

Oh, I see now. The picture makes a little more sense. If it the springs stretch a mximum of 25 cm.

Then I would use 25 cm for x in the original. So the work done by springs turned out to be 18.24 J. Is this right?

I still can't figure out how to solve for how far it goes up. Are the lengths of strings involved in this?

 

[Q_Goest]

Oh, I see now. The picture makes a little more sense. If it the springs stretch a mximum of 25 cm.

Then I would use 25 cm for x in the original. So the work done by springs turned out to be 18.24 J. Is this right?

I still can't figure out how to solve for how far it goes up. Are the lengths of strings involved in this?

I don't get 18.24 J. You had the right equations written before here:

For the original, when they're in series:

W = 2(.5)kx2
W = 2(.5)(400)(.26)2
W = 27.04 J

The final:

W = 2(.5)kx2
W = 2(.5)(400)(.13)2
W = 6.76 J

Because each spring is supporting half the weight, the distance stretched is 0.13

So I subtracted the final from the original and got 20.28

except now the initial isn't .26, it's .025, so the total difference is:
The initial:
W = 2(.5)kx2
W = 2(.5)(400)(.025)2
W = ? J

The final:

W = 2(.5)kx2
W = 2(.5)(400)(.13)2
W = 6.76 J

 

[musicfairy]

So I'll use 25 cm for the original stretch
W = 2(.5)kx²
W = 2(.5)(400)(.25)²
W = 25 J

25 - 6.76 = 18.24

That's where I got 18.24 J from.

 

[Q_Goest]

So I'll use 25 cm for the original stretch
W = 2(.5)kx²
W = 2(.5)(400)(.25)²
W = 25 J

25 - 6.76 = 18.24

That's where I got 18.24 J from.

Your decimal place is in the wrong spot. It's 25 cm, not .25 m. ...

W = 2(.5)kx²
W = 2(.5)(400)(.025)²
W = 25 J

.25 - 6.76 = -6.51 J

or the springs do a total of 6.51 J of work on the box.

Note that the box actually falls. I don't see any way around this conclusion. The spring after cutting the short cord stretches 130 cm. So the total length of each string/spring combination that is now in parallel after cutting is:
Length of spring: 50 cm
Length of string: 85 cm
Stretch of spring: 130 cm (actually, 131 cm)
Total: 50 + 85 + 130 = 265 cm

The box was originally at 160 cm (85 cm + 85 cm - 10 cm) so the box drops 105 cm after cutting the string.

 

[musicfairy]

Doesn't 25 cm = 0.25 m?

That's strange. One of the questions was whether the box moves up or down. I chose up and that's correct.

 

[Q_Goest]

Hi music... I have to apologize. I had a tremendous brain fart. I was seeing cm but thinking mm for some reason... :yuck: <sorry>

ok, back to the question. Yes, I calculate the box rises after you cut the string. (helps to use the right units) The 85 cm string does NOT go taut.

You already know how to calculate the potential energy in the springs, you did it correctly here:

For the original, when they're in series:

W = 2(.5)kx2
W = 2(.5)(400)(.26)2
W = 27.04 J

The final:

W = 2(.5)kx2
W = 2(.5)(400)(.13)2
W = 6.76 J

Because each spring is supporting half the weight, the distance stretched is 0.13

So I subtracted the final from the original and got 20.28

So the difference in the stored spring energy is correct, but then you said:

Apparently 20.28 didn't work for part c. Something's wrong...

If the answer to C is not 20.28 J then perhaps they're asking for the total change in energy of the box. I suppose one could say this change in energy of the box is due to the springs, so we could find the difference in height the box moves when we cut the spring and equate that.

The initial distance the box hangs below the ceiling is what you've already calculated:
50 cm + 10 cm + 50 cm + 2*26 cm = 172 cm (1.72 m)

The final distance the box hangs below the ceiling is also what you've calculated for a single spring/string combo:
50 cm + 85 cm + 13 cm = 148 cm (1.48 m)

check my math, don't want another brain fart here! lol

ok, so the box rises from 1.72 to 1.48 or .24 m (24 cm).

What's the potential energy change of a box that weighs 105 N and rises 24 cm?

 

[musicfairy]

I see your reasoning. It makes a lot of sense.

So I got 162 cm for the initial length, 148 for the final and a change of 14, but apparently 14cm doesn't work.

 

[Q_Goest]

oh wait...

spring is 50 cm
stretch is 26 cm
string in center is 10 cm

that's 86 cm

but the string holding those two points is 85 cm.

Does that help?

 

[musicfairy]

I finally got it right! It turned out that I rounded in my previous answer. The change in length is 14.375 cm instead of 14 cm. For part b I multiplied that by 105 N and got 15.09 J.

Thank you so much for all your help.