2 trucks pulling a third truck by the means of a pulley

AI Thread Summary
The discussion revolves around determining the acceleration of a third truck being towed by two others using a pulley system. Participants clarify that the problem can be approached through kinematics rather than forces, emphasizing the importance of the constant length of the rope. They derive relationships between the distances and accelerations of the trucks, leading to the conclusion that the acceleration of the third truck is the average of the two towing trucks' accelerations. The conversation highlights the elegance of using kinematic constraints to solve the problem effectively. Overall, the method of relating distances and accelerations proves to be a key insight in solving the towing scenario.
Jkyou
Messages
6
Reaction score
0

Homework Statement


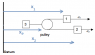
Two trucks tow a third one by means of inextensible ropes and a pulley attached to them (fig. 1). The accelerations of the two trucks are a1 and a2. What is the acceleration of the third truck that is being towed?
(fig.1) is in this link (I'm sorry, I don't know how to post images on websites):
http://www.physics.ox.ac.uk/olympiad/Downloads/PastPapers/BPhO_AS_2007_QP.pdf

m=mass of truck
a1,a2 respective accelerations
a=the shared acceleration (whole system)
T= Tension

Homework Equations


F = ma
Free body diagrams

The Attempt at a Solution


Although the problem didn't specify, I'm assuming the masses of the trucks are equal
Since the total acceleration of the two trucks must be the same,

2ma = ma1-ma2
Thus, a= (a1-a2)/2
Furthermore, ma =T - ma2 for the second truck, so

T = ma + ma2 -> T = m(a1+a2)/2

The force of the tension on the pulley and 3rd truck = 2T

And total force on the pulley, which pulls the third truck = ma

Thus ma = 2T -> a = a1+a2, but the answer key says it's a = (a1+a2)/2
 
Physics news on Phys.org
Hello. Welcome to PF!

The accelerations of trucks 1 and 2 are not necessarily the same. This is a kinematics problem. You do not need to work with forces.

For problems like this, it is often helpful to use the fact that the total length of a rope must remain constant. Consider introducing distances from a fixed line ("datum") as shown below. Can you relate the distances x1, x2, and xp to the length of the rope connecting trucks 1 and 2?
 

Attachments

  • three trucks.png
    three trucks.png
    2.5 KB · Views: 1,147
So that'll be length = x1 + x2 -2xp ?
 
TSny said:
Hello. Welcome to PF!

The accelerations of trucks 1 and 2 are not necessarily the same. This is a kinematics problem. You do not need to work with forces.

For problems like this, it is often helpful to use the fact that the total length of a rope must remain constant. Consider introducing distances from a fixed line ("datum") as shown below. Can you relate the distances x1, x2, and xp to the length of the rope connecting trucks 1 and 2?

Will it be then length of rope = x1 + x2 - 2xp = constant

And perhaps take the double derivative of that?
 
Jkyou said:
Will it be then length of rope = x1 + x2 - 2xp = constant

And perhaps take the double derivative of that?
Yes!
 
TSny said:
Yes!
Ohh I see! That's a really elegant way to do that. Do you think it's possible with forces, just for the fun of it? Or will it be difficult to do that?
 
Jkyou said:
Ohh I see! That's a really elegant way to do that. Do you think it's possible with forces, just for the fun of it? Or will it be difficult to do that?
The kinematic constraint is what determines the relation between the accelerations, not the forces. But, you can then use the relation between the accelerations and F = ma to relate various forces in the problem.
 
TSny said:
The kinematic constraint is what determines the relation between the accelerations, not the forces. But, you can then use the relation between the accelerations and F = ma to relate various forces in the problem.

I see, so the accelerations are dependent on the constraint and not always on the forces situations such as this one. So for example if I were to determine the tension in the string, since 2T = ma where a must be the acceleration of the pulley, I can determine T = m(a1+a2)/4 and etc. Am I on the right track?
 
Jkyou said:
I see, so the accelerations are dependent on the constraint and not always on the forces situations such as this one. So for example if I were to determine the tension in the string, since 2T = ma where a must be the acceleration of the pulley, I can determine T = m(a1+a2)/4 and etc. Am I on the right track?
Yes. The details would depend on what information you are given and what you are trying to determine.
 
  • #10
TSny said:
Yes. The details would depend on what information you are given and what you are trying to determine.

Ahh I see, thank you so much! I am glad I came here for help ^^
 
  • #11
OK. Glad I could help.
 
  • #12
TSny said:
Yes!
How do you take the double derivate of that and come to the answer?
 
  • #13
Seneka said:
How do you take the double derivate of that and come to the answer?
Welcome to PF!

Please write out the specific equation that you wish to differentiate.
 
  • #14
TSny said:
Welcome to PF!

Please write out the specific equation that you wish to differentiate.

The one used to answer the question above...so x1+x2-2xp.I get that the length of the rope is x1+x2-2xp but I don't understand how you differentiated it and how that led to the answer.
 
  • #15
Seneka said:
I get that the length of the rope is x1+x2-2xp but I don't understand how you differentiated it and how that led to the answer.
So the equation is L = x1 + x2 - 2xp, where L is the length of the rope. What do you get if you take one time derivative of each side?
 
  • #16
TSny said:
So the equation is L = x1 + x2 - 2xp, where L is the length of the rope. What do you get if you take one time derivative of each side?

I don't know.
 
  • #17
What does the time derivative of x1 represent?
 
  • #18
TSny said:
What does the time derivative of x1 represent?

Velocity?
 
  • #19
Seneka said:
Velocity?
Yes. So, you could write the time derivative of x1 as v1.
 
  • #20
Where are you going with this?

So, x1+x2-2xp=l
v1+v2-2vp=vl?
a1+a2-2ap=al?
a1+a2-al=2ap?
(a1+a2-al)/2=ap?
 
  • #21
Seneka said:
Where are you going with this?
Hopefully to some insight :oldsmile:

So, x1+x2-2xp=l
v1+v2-2vp=vl?
What does vl represent? The ropes are given to be "inextensible".
What does this imply about the right hand side of your equation x1+x2-2xp=l?
 
  • #22
TSny said:
Hopefully to some insight :oldsmile:

I appreciate your patience.

What does vl represent? The ropes are given to be "inextensible".
What does this imply about the right hand side of your equation x1+x2-2xp=l?

vl=0 there is no change is l
you could rearrange to get vp=(v1+v2)/2
I guess if you do the second derivative you get ap=(a1+a2)/2
Am I right?
 
  • #23
Seneka said:
vl=0 there is no change is l
you could rearrange to get vp=(v1+v2)/2
I guess if you do the second derivative you get ap=(a1+a2)/2
Am I right?
Yes. Good work.
 
  • #24
TSny said:
Yes. Good work.

OMD! I finally got there. Thanks again for your patience and quick reply! Is there a name for this technique using this 'datum' thing or is it just logic?
 
  • #25
I don't know of any name for the technique.
 

Similar threads

Finding acceleration in multiple pulley system
Replies
1
Views
5K
What if check: Am I calculating tension wrong?
Replies
3
Views
2K
Why is tension (T) only added to one side of an Atwood Machine?
Replies
3
Views
2K
Tension in a string which connects 3 pulleys
Replies
12
Views
1K
Laws of Motion (Pulleys, blocks)
Replies
21
Views
9K
Problem with pulleys - two fixed and one movable
Replies
22
Views
313
Understanding Newton's Third Law in Action: A Truck Pushing an SUV
Replies
4
Views
2K
Double pulley Atwood machine (with 3 masses)
2
Replies
97
Views
16K
Newton's laws of motion -- Constaint motion
Replies
13
Views
4K
Block connected to 2 real pulleys
Replies
18
Views
761

Hot Threads

Recent Insights

Back
Top