3 Pulleys System, find the acceleration of both mass.

[Bonten]

Homework Statement

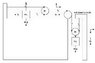
Here is a picture that I putted together(see attached picture).
m1= 0.235 kg
N = m1g = 2.303 N
m2= 0.350 kg
m2g = 3.430 N
fk= 0.590 N

By measurement, I confirmed (d1)=4(d2).
Therefore, (v1)=4(v2), a1= 4(a2).

Homework Equations

ƩFx=(T1)-fk=(m1)(a1)
ƩFy=(m2)g-(T2)/2=(m2)(a2)
(T2)-4(T1)=0

The Attempt at a Solution

Try to find a1 and a2.
[(m2)g-(m2)a2)]/2-fk=(m1)4(a2)
1.715-0.175(a2)-0.590=(.235)(4)(a2)
1.125=1.115(a2)
(a2)=1.01 m/s^2
(a1)=4.036m/s^2

please correct me if I am wrong. Thank you.

 

[ehild]

By measurement, I confirmed (d1)=4(d2).
Therefore, (v1)=4(v2), a1= 4(a2).

Homework Equations

ƩFx=(T1)-fk=(m1)(a1)
ƩFy=(m2)g-(T2)/2=(m2)(a2)
(T2)-4(T1)=0please correct me if I am wrong. Thank you.

Hi Bonten!

The expressions in red are not right. Think them over.ehild

 

[Bonten]

I got hang up on this all weekend.
1)would it be ƩFy=(m2)g-(T2)=(m2)(a2) ?
2)would (T2)-2(T1)=0 ? since T2 exerted the force from (m2)(g2) to the pulley (P1) which divided the tension by 2.
3)but the T2 got divided by 2 by the pulley P2 which directly attached with m2. here is the diagram, it applies with p1 pulley as well.

 

[Bonten]

http://upload.wikimedia.org/wikipedia/commons/b/bb/Pulley1.svg

 

[ehild]

I got hang up on this all weekend.
1)would it be ƩFy=(m2)g-(T2)=(m2)(a2) ?

No. Two pieces of string act upward, each with tension T₂. m₂g-2T₂=m₂a.

2)would (T2)-2(T1)=0 ? since T2 exerted the force from (m2)(g2) to the pulley (P1) which divided the tension by 2.

Yes, the pulley is massless so the sum of forces acting to it must be zero. 2T₁ acts to the left and T₂ acts to the right: T₂-2T₁=0.

3)but the T2 got divided by 2 by the pulley P2 which directly attached with m2. here is the diagram, it applies with p1 pulley as well.

Your diagram applies for equilibrium, when W-2T=0, so T=W/2.



ehild

 

[azizlwl]

It can be seen clearly in your diagram, 2×T2 is opposing the motion of M2.

 

[Bonten]

this is system not quite in equilibrium, since the downward motion of m₂g will create an acceleration for the whole system, but a² will be 4 times smaller than a¹.