Relationship of acceleration of masses in pulley

AI Thread Summary
The discussion focuses on determining the relationship of acceleration between three masses (m1, m2, and m3) in a pulley system, where m1 is greater than m2, which is greater than m3. Participants share their equations, with one suggesting a1 - a2 + 2(a3) = 0 and another proposing 2(a1) - 2(a2) - a3 = 0, leading to confusion about the correct setup without a visual aid. The conversation highlights the movement dynamics, noting that m1 and m2 cannot both move downward simultaneously, as this would affect the position of m3. The professor's guidance emphasizes finding displacement to solve the equations, suggesting that m2 and m3 move upward while m1 moves downward. The discussion concludes with the acknowledgment of specific mass values for each object, which adds context to the problem.
drragonx
Messages
12
Reaction score
0

Homework Statement


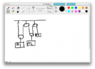
Find the relationship of acceleration between the masses, m1, m2 and m3 where m1>m2>m3.

The question has a free pulley in the left attached to mass m1. then goes through a fixed pulley , through a free pulley that is attached to m2 and then through a fixed pulley, with the end of the string attached to mass m3.

Homework Equations

The Attempt at a Solution


my professor came up with: a1-a2+2(a3)=0 while i came up with 2(a1)-2(a2)-a3=0
 
Physics news on Phys.org
Without a drawing it's difficult to "see" the setup.
What "goes" through a fixed pulley? Not the free pulley, I suppose.
Isn't the rope attached to a wall or ceiling on the left?
 
heres the image
 

Attachments

  • Screen Shot 2014-10-06 at 2.28.04 PM.png
    Screen Shot 2014-10-06 at 2.28.04 PM.png
    37 KB · Views: 505
Are you allowed to use a Lagrangian? Or just N2L?
 
(Also, that would be good info to put under relevant equations)
 
I think m3 have the larger acceleration so your equation looks better to me.
However the signs do not look so good.
If both m1 and m2 move with the same acceleration (downwards for example) it would result that a3 is zero which is not what happens.
 
m1 and m2 cannot both move downward. the only way m1 can move down is if m2 moves up, giving m1 the freedom to move down (it can't move down without taking the rope with it)
 
Yes, they can. They both "take rope" from m3 which moves up.
It depends on the masses.
 
Hmmm... somehow I neglected the fact that m1 and m2 were held up via pulleys attached to them... sorry about that.
 
  • #10
as per my prof's explanation, we are allowed to assume any sensible motion for the masses. so here, both equations assume m2 and m3 are moving up while m1 is moving down. The general method to solve these equations, as per my prof's suggestion, is to find the displacement. So, for the following question, 2(x2)=x1+x3, which when differentiated becomes 2(a2)=(a1)+(a3)
 

Attachments

  • Screen Shot 2014-10-06 at 8.50.06 PM.png
    Screen Shot 2014-10-06 at 8.50.06 PM.png
    58.2 KB · Views: 520
  • #11
But this is a different problem. Are you done with the first one?
 
  • #12
im just saying they both are related in the way we solve them. This question's answer is certain but not the first one. I posted the question so that you get the idea of it.
 
  • #13
also, i recently found out that m1=16kg, m2=8kg, m3=2kg
 

Similar threads

Using Effective Mass to find the accelerations of 3 masses connected by pulleys
Replies
25
Views
3K
Olympiad dynamics problem with 3 masses and a pulley
Replies
17
Views
2K
Accelerating pulleys (3 pulleys and 3 masses)
Replies
5
Views
2K
Double pulley Atwood machine (with 3 masses)
2
Replies
97
Views
16K
Newton's Second Law (Pulley Sustem)
Replies
3
Views
2K
Calculating tensions and acceleration
Replies
10
Views
2K
Pulley system problem: 6 Pulleys and 1 Mass
Replies
5
Views
858
3 pulley problem with attached masses
Replies
15
Views
5K
What Are the Accelerations and Tensions in a Double Atwood's Machine System?
Replies
8
Views
10K
Pulley Problem: Find the acceleration of M2 & M3
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top