A balloon and a springfind extension

[brunettegurl]

Homework Statement

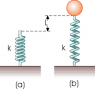
A light spring of constant k = 85.0 N/m rests vertically on a table (as shown in part a) of the figure below). A 2.25 g balloon is filled with helium (density = 0.180 kg/m3) to a volume of 5.95 m3 and is then connected to the spring, causing it to stretch as shown in part b). Determine the extension distance L when the balloon is in equilibrium.

Homework Equations

F= k\Deltax
F=\rhoA

The Attempt at a Solution

so i tried to find the weight of the balloon by multiplying Volume of the balloon to the density to the density and then adding it to the mass of the balloon and multiplying it to 9.8m/s². this answer of 10.51785 i divided by k (85N/m) and got an answer of 0.124 m..this was wrong ..can someone tell me what is wrong with this thinking

 

[cepheid]

What's wrong with this thinking is that the weight of the balloon is NOT the force that is pulling UP on the spring to stretch it. You need to figure out with what force your balloon is being pushed upward.

 

[brunettegurl]

would it be the difference of the weight of the balloon and the air that it displaces to stretch the spring upward??