DrVirz
- 24
- 0
Hi all,
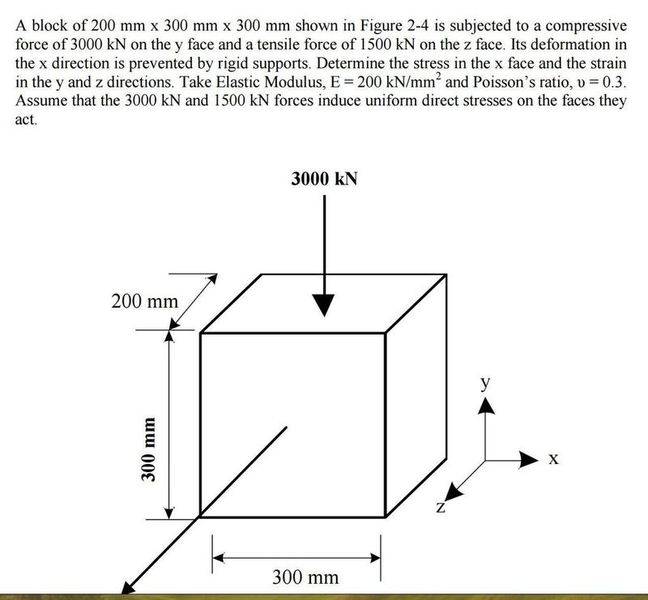
Having some trouble getting the final answer on the question below, the fact that the cube doesn't have a force in the x direction is throwing me off. Once I fine the force(??) in the x-direction, I can just use the generalized Hooke's law to obtain strain? Any help is appreciated.
2. Equations in upload of solution.
See my solution for relevant equations.
http://[ATTACH=full]199721[/ATTACH]
Having some trouble getting the final answer on the question below, the fact that the cube doesn't have a force in the x direction is throwing me off. Once I fine the force(??) in the x-direction, I can just use the generalized Hooke's law to obtain strain? Any help is appreciated.
Homework Statement
2. Equations in upload of solution.
See my solution for relevant equations.
http://[ATTACH=full]199721[/ATTACH]
Attachments
Last edited by a moderator:
