- #1
BiGyElLoWhAt
Gold Member
- 1,622
- 131
Homework Statement
Write a program to find the equivalent resistance between two opposite corners within a grid of "infinite size" with resistors between each point.
So basically we have an infinite cube made up of cubes with 1 ohm resistors between each node.
Homework Equations
Kirkoff's laws
The Attempt at a Solution
Really what I'm having problems with is defining the direction of the current in a way that is consistent and allows every point a path from V+ to V-=0
I'm using a 1001x1001x1001 array that will hold the coefficients for each kirkoffs current law at each point. I am setting 500,500, 500 = V+ and 501,501,501 = 0 V (so it's symmetric about the central cube of resistors).
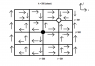
What I'm doing so far,I have k=500 and drew a plane and sketched out the current paths.
I have for the current direction: (it won't let me put pseudocode as the language)
Code:
#for the i direction of current
if j<= 500
if i < 500
I = -i # (meaning I take V(i+1,j,500) to be higher V than V(i,j,500)
if i >500
I = + i #(Vi > Vi+1)
if i=500
I = -+ i # (V(500,j,500) > V(501,j,500) && V(499,j,500) (I is - i to the left and + i to the right)
if j = 501
if i < 501
I = + i
if i = 501
I = +-i #V( 501,501,500) < all adjacent points except for V(501,501,501) ) (I is +i to the left and -i to the right)
if i > 501
I = -i
if j > 501
I = +iThis feels like a bit overkill, so my question, is there a better way to write this?
Really all I need is for every point to have a complete path to 501,501,501 and a complete path from 500,500,500 to that point. Additionally, I need 500,500,500 to send out current in all directions and 501,501,501 to take current from all directions.
In the picture, the arrows indicate the current flow, the solid circle indicates that the point is V+ and the empty circle indicates that V- = 0 is in the adjacent plane.
***Edit***
I changed the current flow direction from 499,501,500 -> 500,502,500 to be in the opposite direction so that I have less cases to handle for the j direction.
***Edit again***
Crap, I think I need a 6d array, 3d for the point and 3d for the coefficients...
So I'll basically have ##V_{ijklmn}V^{lmn} = B_{ijk}##
There's got to be something stupid I'm doing.
***Edit numero tres***
So with the 6d array, the biggest I can make it on my pc is 17^6, otherwise I get a memory error. I might be able to make it a couple points larger if I close everything out, but I don't think 17^3 cube is large enough to get a reasonable approximation. Any suggestions?
**4**
I just allocated 16Gb to a paging file, and now I can go to 19^6 lol... 21 still gives me a memory error, though.
**5**
So I'm not using any quantity of my memory. A 17^3 array of zeros is about 184 Mb. (193100552 bytes)/(1024^2)
Attachments
Last edited: